
【题目】在平面直角坐标系xOy中,二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,则下列结论正确的是( ) 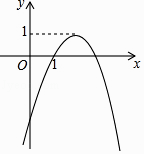
A.a<0,b<0,c>0
B.﹣ ![]() =1
=1
C.a+b+c<0
D.关于x的方程x2+bx+c=﹣1有两个不相等的实数根
【答案】D
【解析】解:A、错误.a<0,b>0,c<0. B、错误.﹣ ![]() >1.
>1.
C、错误.x=1时,y=a+b+c=0.
D、正确.观察图象可知抛物线y=ax2+bx+c与直线y=﹣1有两个交点,所以关于x的方程x2+bx+c=﹣1有两个不相等的实数根.
故选D.
【考点精析】本题主要考查了求根公式和二次函数图象以及系数a、b、c的关系的相关知识点,需要掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,直线l的解析式为y=﹣x+4,它与x轴和y轴分别相交于A,B两点.平行于直线l的直线m从原点O出发,沿x轴的正方向以每秒1个单位长度的速度运动.它与x轴和y轴分别相交于C,D两点,运动时间为t秒(0≤t≤4),以CD为斜边作等腰直角三角形CDE(E,O两点分别在CD两侧).若△CDE和△OAB的重合部分的面积为S,则S与t之间的函数关系的图象大致是( )
A.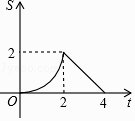
B.
C.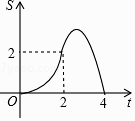
D.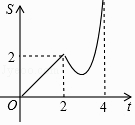
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=36°,DE是线段AC的垂直平分线,若BE=a,AE=b,则用含a、b的代数式表示△ABC的周长为 . 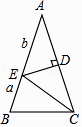
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解全校学生上学期参加“生涯规划”社区活动的情况,学校随机调查了本校50名学生参加社区活动的次数,并将调查所得的数据整理如下:
参加社区活动次数的频数、频率
活动次数x | 频数 | 频率 |
0<x≤3 | 10 | 0.20 |
3<x≤6 | a | 0.24 |
6<x≤9 | 16 | 0.32 |
9<x≤12 | 6 | 0.12 |
12<x≤15 | b | m |
15<x≤18 | 2 | n |
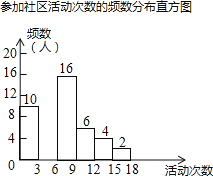
根据以上图表信息,解答下列问题:
(1)表中a= , b= , m= , n= .
(2)请把频数分布直方图补充完整(画图后请标注相应的数据);
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线y=x+1与抛物线y=2x2相交于A、B两点,与y轴交于点M,M、N关于x轴对称,连接AN、BN.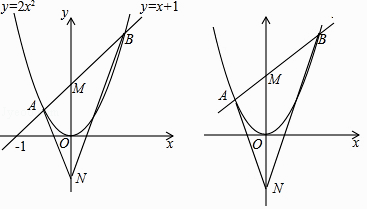
(1)①求A、B的坐标;②求证:∠ANM=∠BNM;
(2)如图2,将题中直线y=x+1变为y=kx+b(b>0),抛物线y=2x2变为y=ax2(a>0),其他条件不变,那么∠ANM=∠BNM是否仍然成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ACB中,∠ACB=90°,点D是AB的中点,点E是CD的中点,过点C作CF∥AB叫AE的延长线于点F. 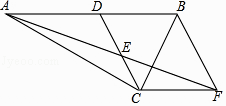
(1)求证:△ADE≌△FCE;
(2)若∠DCF=120°,DE=2,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
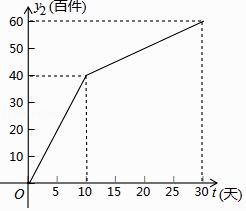
【题目】我市雷雷服饰有限公司生产了一款夏季服装,通过实体商店和网上商店两种途径进行销售,销售一段时间后,该公司对这种商品的销售情况,进行了为期30天的跟踪调查,其中实体商店的日销售量y1(百件)与时间t(t为整数,单位:天)的部分对应值如下表所示,网上商店的日销售量y2(百件)与时间t(t为整数,单位:天)的部分对应值如图所示.
时间t(天) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
日销售量 | 0 | 25 | 40 | 45 | 40 | 25 | 0 |
(1)请你在一次函数、二次函数和反比例函数中,选择合适的函数能反映y1与t的变化规律,并求出y1与t的函数关系式及自变量t的取值范围;
(2)求y2与t的函数关系式,并写出自变量t的取值范围;
(3)在跟踪调查的30天中,设实体商店和网上商店的日销售总量为y(百件),求y与t的函数关系式;当t为何值时,日销售总量y达到最大,并求出此时的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=k1x-3(k1>0)的图象与x轴、y轴分别交于A,B两点,
与反比例函数y=![]() (k2>0)的图象交于C,D两点,作CE⊥y轴,垂足为点E,作DF⊥y轴,垂足为点F,已知CE=1.
(k2>0)的图象交于C,D两点,作CE⊥y轴,垂足为点E,作DF⊥y轴,垂足为点F,已知CE=1.
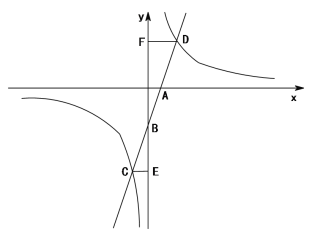
(1) ①直接写出点C的坐标 (用k1来表示)
②k2﹣k1= ;
(2) 若B为AC的中点,求反比例函数的表达式;
(3) 在(2)的条件下,设点M是x轴负半轴上一点,将线段MF绕点M按顺时针或逆时针方向旋转90°得到线段MN,当点M滑动时,点N能否在反比例函数的图象上?如果能,求出点N的坐标;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=16,O为AB中点,点C在线段OB上(不与点O,B重合),将OC绕点O逆时针旋转270°后得到扇形COD,AP,BQ分别切优弧 ![]() 于点P,Q,且点P,Q在AB异侧,连接OP.
于点P,Q,且点P,Q在AB异侧,连接OP. 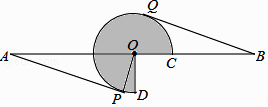
(1)求证:AP=BQ;
(2)当BQ=4 ![]() 时,求
时,求 ![]() 的长(结果保留π);
的长(结果保留π);
(3)若△APO的外心在扇形COD的内部,求OC的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com