
½Ģ²ÄµŚ66Ņ³Ģ½Ė÷Ę½·½²ī¹«Ź½Ź±ÉčÖĆĮĖČēĻĀĒé¾³£ŗ±ß³¤ĪŖbµÄŠ”Õż·½ŠĪÖ½Ę¬·ÅÖĆŌŚ±ß³¤ĪŖaµÄ“óÕż·½ŠĪÖ½Ę¬ÉĻ£ØČēĶ¼9?6£©£¬ÄćÄÜĶعż¼ĘĖćĪ“øĒ×”²æ·ÖµÄĆ껿µĆµ½¹«Ź½(a + b) (a?b) = a2?b2Āš£æ£Ø²»±ŲÖ¤Ć÷£©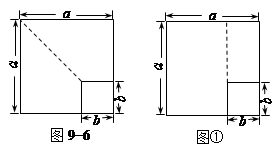
(1)Čē¹ū½«Š”Õż·½ŠĪµÄŅ»±ßŃÓ³¤£ØČēĶ¼¢Ł£©£¬ŹĒ·ńŅ²ÄÜĶʵ¼¹«Ź½£æĒėĶź³ÉÖ¤Ć÷£®
(2) Ć껿·Ø³żĮĖæÉŅŌ°ļÖśĪŅĆĒ¼ĒŅ乫Ź½£¬»¹æÉŅŌÖ±¹ŪµŲĶʵ¼»ņŃéÖ¤¹«Ź½£¬Ė×³Ę”°ĪŽ×ÖÖ¤Ć÷”±£®ĄżČē£¬ÖųĆūµÄÕŌĖ¬ĻŅĶ¼£ØČēĶ¼¢Ś£¬ĘäÖŠĖÄøöÖ±½ĒČż½ĒŠĪ½Ļ“óµÄÖ±½Ē±ß³¤¶¼ĪŖa£¬½ĻŠ”µÄÖ±½Ē±ß³¤¶¼ĪŖb£¬Š±±ß³¤¶¼ĪŖc£©£¬“óÕż·½ŠĪµÄĆ껿æÉŅŌ±ķŹ¾ĪŖc2£¬Ņ²æÉŅŌ±ķŹ¾ĪŖ4´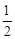 ab + (a ?b)2£¬ÓÉ“ĖĶʵ¼³öÖŲŅŖµÄ¹“¹É¶ØĄķ£ŗa2 + b2 = c2£®Ķ¼¢ŪĪŖĆĄ¹śµŚ¶žŹ®ČĪ×ÜĶ³Ł¤·Ę¶ūµĀµÄ”°×ÜĶ³Ö¤·Ø”±£¬ĒėÄćĶź³ÉÖ¤Ć÷£®
ab + (a ?b)2£¬ÓÉ“ĖĶʵ¼³öÖŲŅŖµÄ¹“¹É¶ØĄķ£ŗa2 + b2 = c2£®Ķ¼¢ŪĪŖĆĄ¹śµŚ¶žŹ®ČĪ×ÜĶ³Ł¤·Ę¶ūµĀµÄ”°×ÜĶ³Ö¤·Ø”±£¬ĒėÄćĶź³ÉÖ¤Ć÷£®
(3) ŹŌ¹¹ŌģŅ»øöĶ¼ŠĪ£¬Ź¹ĖüµÄĆ껿Äܹ»½āŹĶ(a? 2b)2 = a2?4ab + 4b2£¬»ŌŚĻĀĆęµÄøńµćÖŠ£¬²¢±ź³ö×ÖÄøa”¢bĖł±ķŹ¾µÄĻ߶Ī£®
 æŚĖćĢāĢģĢģĮ·ĻµĮŠ“š°ø
æŚĖćĢāĢģĢģĮ·ĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
| 1 | 2 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ2011-2012ѧğ½ĖÕŹ”Ģ«²ÖŹŠĘßÄź¼¶ĻĀŃ§ĘŚĘŚÖŠæ¼ŹŌŹżŃ§ŹŌ¾ķ£Ø“ų½āĪö£© ĢāŠĶ£ŗ½ā“šĢā
½Ģ²ÄµŚ66Ņ³Ģ½Ė÷Ę½·½²ī¹«Ź½Ź±ÉčÖĆĮĖČēĻĀĒé¾³£ŗ±ß³¤ĪŖbµÄŠ”Õż·½ŠĪÖ½Ę¬·ÅÖĆŌŚ±ß³¤ĪŖaµÄ
“óÕż·½ŠĪÖ½Ę¬ÉĻ£ØČēĶ¼9?6£©£¬ÄćÄÜĶعż¼ĘĖćĪ“øĒ×”²æ·ÖµÄĆ껿µĆµ½¹«Ź½(a + b) (a ? b) = a2? b2Āš£æ
£Ø²»±ŲÖ¤Ć÷£©
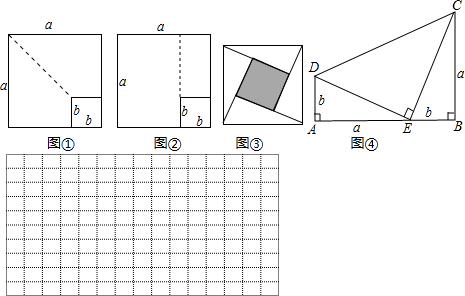
(1)Čē¹ū½«Š”Õż·½ŠĪµÄŅ»±ßŃÓ³¤£ØČēĶ¼¢Ł£©£¬ŹĒ·ńŅ²ÄÜĶʵ¼¹«Ź½£æĒėĶź³ÉÖ¤Ć÷£®
(2) Ć껿·Ø³żĮĖæÉŅŌ°ļÖśĪŅĆĒ¼ĒŅ乫Ź½£¬»¹æÉŅŌÖ±¹ŪµŲĶʵ¼»ņŃéÖ¤¹«Ź½£¬Ė×³Ę”°ĪŽ×ÖÖ¤Ć÷”±£®ĄżČē£¬ÖųĆūµÄÕŌĖ¬ĻŅĶ¼£ØČēĶ¼¢Ś£¬ĘäÖŠĖÄøöÖ±½ĒČż½ĒŠĪ½Ļ“óµÄÖ±½Ē±ß³¤¶¼ĪŖa£¬½ĻŠ”µÄÖ±½Ē±ß³¤¶¼ĪŖb£¬Š±±ß³¤¶¼ĪŖc£©£¬“óÕż·½ŠĪµÄĆ껿æÉŅŌ±ķŹ¾ĪŖc2£¬Ņ²æÉŅŌ±ķŹ¾ĪŖ4´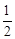 ab + (a ? b)2£¬ÓÉ“ĖĶʵ¼³öÖŲŅŖµÄ¹“¹É¶ØĄķ£ŗa2 + b2 = c2£®
ab + (a ? b)2£¬ÓÉ“ĖĶʵ¼³öÖŲŅŖµÄ¹“¹É¶ØĄķ£ŗa2 + b2 = c2£®
Ķ¼¢ŪĪŖĆĄ¹śµŚ¶žŹ®ČĪ×ÜĶ³Ł¤·Ę¶ūµĀµÄ”°×ÜĶ³Ö¤·Ø”±£¬ĒėÄćĶź³ÉÖ¤Ć÷£®

(3) ŹŌ¹¹ŌģŅ»øöĶ¼ŠĪ£¬Ź¹ĖüµÄĆ껿Äܹ»½āŹĶ(a ? 2b)2 = a2? 4ab + 4b2£¬»ŌŚĻĀĆęµÄøńµćÖŠ£¬²¢±ź³ö×ÖÄøa”¢bĖł±ķŹ¾µÄĻ߶Ī£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ2014½ģ½ĖÕŹ”Ģ«²ÖŹŠĘßÄź¼¶ĻĀŃ§ĘŚĘŚÖŠæ¼ŹŌŹżŃ§ŹŌ¾ķ£Ø½āĪö°ę£© ĢāŠĶ£ŗ½ā“šĢā
½Ģ²ÄµŚ66Ņ³Ģ½Ė÷Ę½·½²ī¹«Ź½Ź±ÉčÖĆĮĖČēĻĀĒé¾³£ŗ±ß³¤ĪŖbµÄŠ”Õż·½ŠĪÖ½Ę¬·ÅÖĆŌŚ±ß³¤ĪŖaµÄ
“óÕż·½ŠĪÖ½Ę¬ÉĻ£ØČēĶ¼9−6£©£¬ÄćÄÜĶعż¼ĘĖćĪ“øĒ×”²æ·ÖµÄĆ껿µĆµ½¹«Ź½(a + b) (a − b) = a2 − b2Āš£æ
£Ø²»±ŲÖ¤Ć÷£©
(1)Čē¹ū½«Š”Õż·½ŠĪµÄŅ»±ßŃÓ³¤£ØČēĶ¼¢Ł£©£¬ŹĒ·ńŅ²ÄÜĶʵ¼¹«Ź½£æĒėĶź³ÉÖ¤Ć÷£®

(2) Ć껿·Ø³żĮĖæÉŅŌ°ļÖśĪŅĆĒ¼ĒŅ乫Ź½£¬»¹æÉŅŌÖ±¹ŪµŲĶʵ¼»ņŃéÖ¤¹«Ź½£¬Ė×³Ę”°ĪŽ×ÖÖ¤Ć÷”±£®ĄżČē£¬ÖųĆūµÄÕŌĖ¬ĻŅĶ¼£ØČēĶ¼¢Ś£¬ĘäÖŠĖÄøöÖ±½ĒČż½ĒŠĪ½Ļ“óµÄÖ±½Ē±ß³¤¶¼ĪŖa£¬½ĻŠ”µÄÖ±½Ē±ß³¤¶¼ĪŖb£¬Š±±ß³¤¶¼ĪŖc£©£¬“óÕż·½ŠĪµÄĆ껿æÉŅŌ±ķŹ¾ĪŖc2£¬Ņ²æÉŅŌ±ķŹ¾ĪŖ4´ ab
+ (a − b)2£¬ÓÉ“ĖĶʵ¼³öÖŲŅŖµÄ¹“¹É¶ØĄķ£ŗa2 +
b2 = c2£®
ab
+ (a − b)2£¬ÓÉ“ĖĶʵ¼³öÖŲŅŖµÄ¹“¹É¶ØĄķ£ŗa2 +
b2 = c2£®
Ķ¼¢ŪĪŖĆĄ¹śµŚ¶žŹ®ČĪ×ÜĶ³Ł¤·Ę¶ūµĀµÄ”°×ÜĶ³Ö¤·Ø”±£¬ĒėÄćĶź³ÉÖ¤Ć÷£®


(3) ŹŌ¹¹ŌģŅ»øöĶ¼ŠĪ£¬Ź¹ĖüµÄĆ껿Äܹ»½āŹĶ(a − 2b)2 = a2 − 4ab + 4b2£¬»ŌŚĻĀĆęµÄøńµćÖŠ£¬²¢±ź³ö×ÖÄøa”¢bĖł±ķŹ¾µÄĻ߶Ī£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ2014½ģ½ĖÕŹ”Ģ«²ÖŹŠĘßÄź¼¶ĘŚÖŠæ¼ŹŌŹżŃ§¾ķ£Ø½āĪö°ę£© ĢāŠĶ£ŗ½ā“šĢā
½Ģ²ÄµŚ66Ņ³Ģ½Ė÷Ę½·½²ī¹«Ź½Ź±ÉčÖĆĮĖČēĻĀĒé¾³£ŗ±ß³¤ĪŖbµÄŠ”Õż·½ŠĪÖ½Ę¬·ÅÖĆŌŚ±ß³¤ĪŖaµÄ“óÕż·½ŠĪÖ½Ę¬ÉĻ£ØČēĶ¼9−6£©£¬ÄćÄÜĶعż¼ĘĖćĪ“øĒ×”²æ·ÖµÄĆ껿µĆµ½¹«Ź½(a + b) (a − b) = a2 − b2Āš£æ£Ø²»±ŲÖ¤Ć÷£©

(1)Čē¹ū½«Š”Õż·½ŠĪµÄŅ»±ßŃÓ³¤£ØČēĶ¼¢Ł£©£¬ŹĒ·ńŅ²ÄÜĶʵ¼¹«Ź½£æĒėĶź³ÉÖ¤Ć÷£®
(2) Ć껿·Ø³żĮĖæÉŅŌ°ļÖśĪŅĆĒ¼ĒŅ乫Ź½£¬»¹æÉŅŌÖ±¹ŪµŲĶʵ¼»ņŃéÖ¤¹«Ź½£¬Ė×³Ę”°ĪŽ×ÖÖ¤Ć÷”±£®ĄżČē£¬ÖųĆūµÄÕŌĖ¬ĻŅĶ¼£ØČēĶ¼¢Ś£¬ĘäÖŠĖÄøöÖ±½ĒČż½ĒŠĪ½Ļ“óµÄÖ±½Ē±ß³¤¶¼ĪŖa£¬½ĻŠ”µÄÖ±½Ē±ß³¤¶¼ĪŖb£¬Š±±ß³¤¶¼ĪŖc£©£¬“óÕż·½ŠĪµÄĆ껿æÉŅŌ±ķŹ¾ĪŖc2£¬Ņ²æÉŅŌ±ķŹ¾ĪŖ4´ ab + (a − b)2£¬ÓÉ“ĖĶʵ¼³öÖŲŅŖµÄ¹“¹É¶ØĄķ£ŗa2 + b2
= c2£®Ķ¼¢ŪĪŖĆĄ¹śµŚ¶žŹ®ČĪ×ÜĶ³Ł¤·Ę¶ūµĀµÄ”°×ÜĶ³Ö¤·Ø”±£¬ĒėÄćĶź³ÉÖ¤Ć÷£®
ab + (a − b)2£¬ÓÉ“ĖĶʵ¼³öÖŲŅŖµÄ¹“¹É¶ØĄķ£ŗa2 + b2
= c2£®Ķ¼¢ŪĪŖĆĄ¹śµŚ¶žŹ®ČĪ×ÜĶ³Ł¤·Ę¶ūµĀµÄ”°×ÜĶ³Ö¤·Ø”±£¬ĒėÄćĶź³ÉÖ¤Ć÷£®

(3) ŹŌ¹¹ŌģŅ»øöĶ¼ŠĪ£¬Ź¹ĖüµÄĆ껿Äܹ»½āŹĶ(a − 2b)2 = a2 − 4ab + 4b2£¬»ŌŚĻĀĆęµÄøńµćÖŠ£¬²¢±ź³ö×ÖÄøa”¢bĖł±ķŹ¾µÄĻ߶Ī£®

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com