
【题目】如图,已知抛物线y=ax2+bx+1经过A(﹣1,0),B(1,1)两点.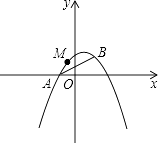
(1)求该抛物线的解析式;
(2)阅读理解:
在同一平面直角坐标系中,直线l1:y=k1x+b1(k1 , b1为常数,且k1≠0),直线l2:y=k2x+b2(k2 , b2为常数,且k2≠0),若l1⊥l2 , 则k1k2=﹣1.
解决问题:
①若直线y=3x﹣1与直线y=mx+2互相垂直,求m的值;
②抛物线上是否存在点P,使得△PAB是以AB为直角边的直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)M是抛物线上一动点,且在直线AB的上方(不与A,B重合),求点M到直线AB的距离的最大值.
【答案】
(1)解:将A,B点坐标代入,得
![]() ,
,
解得 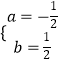 ,
,
抛物线的解析式为y=﹣ ![]() x2+
x2+ ![]() x+1;
x+1;
(2)解:①由直线y=3x﹣1与直线y=mx+2互相垂直,得
3m=﹣1,
即m=﹣ ![]() ;
;
②AB的解析式为y= ![]() x+
x+ ![]() ,
,
当PA⊥AB时,PA的解析式为y=﹣2x﹣2,
联立PA与抛物线,得
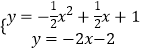 ,
,
解得 ![]() (舍),
(舍), ![]() ,即P(6,﹣14);
,即P(6,﹣14);
当PB⊥AB时,PB的解析式为y=﹣2x+3,
联立PB与抛物线,得 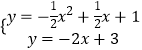 ,
,
解得 ![]() (舍)
(舍) ![]() 即P(4,﹣5),
即P(4,﹣5),
综上所述:△PAB是以AB为直角边的直角三角形,点P的坐标(6,﹣14)(4,﹣5);
(3)解:如图
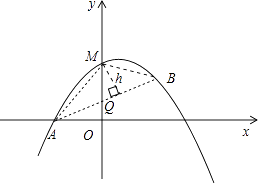 ,
,
∵M(t,﹣ ![]() t2+
t2+ ![]() t+1),Q(t,
t+1),Q(t, ![]() t+
t+ ![]() ),
),
∴MQ=﹣ ![]() t2+
t2+ ![]()
S△MAB= ![]() MQ|xB﹣xA
MQ|xB﹣xA
= ![]() (﹣
(﹣ ![]() t2+
t2+ ![]() )×2
)×2
=﹣ ![]() t2+
t2+ ![]() ,
,
当t=0时,S取最大值 ![]() ,即M(0,1).
,即M(0,1).
由勾股定理,得
AB= ![]() =
= ![]() ,
,
设M到AB的距离为h,由三角形的面积,得
h= ![]() =
= ![]() .
.
点M到直线AB的距离的最大值是 ![]() .
.
【解析】(1)利用待定系数法把A、B两点的坐标代入解析式即可求出a、b;(2)分类讨论,A或B为直角顶点两类,利用“阅读理解”的结论“相互垂直的直线的斜率k 乘积=-1”构建方程,求出直线解析式,再和抛物线联立方程组,得出交点即P坐标;(3)三角形的底边AB是定值,要求距离最大值就须求面积的最大值,须过M点作x轴的垂线,把三角形MAB分割成两个有竖直边的三角形,构建以M的横坐标t 为自变量的函数S,求出其最大值,再利用三角形面积公式,求出此时的点M到AB的距离,就是最大距离.
【考点精析】根据题目的已知条件,利用二次函数的最值的相关知识可以得到问题的答案,需要掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a.


科目:初中数学 来源: 题型:
【题目】课程改革以来,数学老师积极组织学生参与“综合与实践”活动,学校随机调查了七年级部分同学某月参与“综合与实践”活动的时间,并用得到的数据绘制了不完整的统计图(如图所示),根据图中信息可知扇形图中的“1.5小时”部分圆心角是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是等腰△ABC底边BC上的高.点O是AC中点,延长DO到E,使OE=OD,连接AE,CE.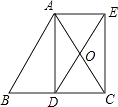
(1)求证:四边形ADCE的是矩形;
(2)若AB=17,BC=16,求四边形ADCE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城市规定:出租车起步价允许行驶的最远路程为3千米,超过3千米的部分按每千米另行收费,甲说:“我乘这种出租车走了9千米,付了15元”:乙说:“我乘这种出租车走了25千米,付了39元”请你算一算这种出租车的起步价是多少元?超过3千米后,每千米的车费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OD是∠AOB的平分线,OE是∠BOC的平分线.
(1)若∠BOC=50°,∠BOA=80°,求∠DOE的度数;
(2)若∠AOC=150°,求∠DOE的度数;
(3)你发现∠DOE与∠AOC有什么等量关系?给出结论并说明.
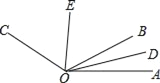
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后解答后面的问题.
我们知道方程2x+3y=12有无数组解,但在实际生活中我们往往只需要求出其正整数解.例:由2x+3y=12,得![]() ,(x、y为正整数)∴
,(x、y为正整数)∴![]() 则有0<x<6.又
则有0<x<6.又![]() 为正整数,则
为正整数,则![]() 为正整数.
为正整数.
由2与3互质,可知:x为3的倍数,从而x=3,代入![]() .
.
∴2x+3y=12的正整数解为![]()
问题:
(1)请你写出方程2x+y=5的一组正整数解:______;
(2)若![]() 为自然数,则满足条件的x值有______个;
为自然数,则满足条件的x值有______个;
A、2B、3C、4D、5
(3)七年级某班为了奖励学习进步的学生,购买了单价为3元的笔记本与单价为5元的钢笔两种奖品,共花费35元,问有几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乘法公式的探究及应用:
数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片边长为![]() 的正方形,B种纸片是边长为
的正方形,B种纸片是边长为![]() 的正方形,C种纸片长为
的正方形,C种纸片长为![]() 宽为
宽为![]() 的长方形,并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形。
的长方形,并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形。
(1)请用两种不同的方法表示图2大正方形的面积:
方法1:_____________________;方法2:_____________________.
(2)观察图2,请你写出下列三个代数式:![]() 之间的等量关系;
之间的等量关系;
(3)类似的,请你用图1中的三种纸片拼一个图形验证:![]()
(4)根据(2)题中的等量关系,解决如下问题:
已知:![]() 求
求![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com