
 如图,甲乙两人在游泳池A处发现游泳池中的P处有人求救,甲立即跳入池中去救人,速度为1米/秒,乙以3.5米/秒的速度沿游泳池边跑到距A不远处的B处,捡起一个游泳圈再跳入池中去救人,甲游了20秒到达P处,两秒后乙到达P处.若∠PAB与∠PBC互余,且cos∠PBC=$\frac{3}{5}$,求乙的游泳速度.
如图,甲乙两人在游泳池A处发现游泳池中的P处有人求救,甲立即跳入池中去救人,速度为1米/秒,乙以3.5米/秒的速度沿游泳池边跑到距A不远处的B处,捡起一个游泳圈再跳入池中去救人,甲游了20秒到达P处,两秒后乙到达P处.若∠PAB与∠PBC互余,且cos∠PBC=$\frac{3}{5}$,求乙的游泳速度. 分析 作PH⊥BC于H.在Rt△PBH中,由cos∠PBH=$\frac{BH}{PB}$=$\frac{3}{5}$,设BH=3k,PB=5k,则PH=4k,由△PBH∽△APH,推出$\frac{PH}{AH}$=$\frac{BH}{PH}$,可得AH=$\frac{16}{3}$k,AB=AH-BH=$\frac{16}{3}$k-3k=$\frac{7}{3}k$,在Rt△APH中,AP=20×1=20,利用勾股定理可得(4k)2+($\frac{16}{3}$k)2=202,求出k即可解决问题.
解答 解: 作PH⊥BC于H.
作PH⊥BC于H.
在Rt△PBH中,∵cos∠PBH=$\frac{BH}{PB}$=$\frac{3}{5}$,设BH=3k,PB=5k,则PH=4k,
∵∠PAB+∠PBC=90°,∠PBC+∠BPH=90°,
∴∠BPH=∠PAH,∵∠PHB=∠PHA,
∴△PBH∽△APH,
∴$\frac{PH}{AH}$=$\frac{BH}{PH}$,
∴$\frac{4k}{AH}$=$\frac{3k}{4k}$,
∴AH=$\frac{16}{3}$k,
∴AB=AH-BH=$\frac{16}{3}$k-3k=$\frac{7}{3}k$,
在Rt△APH中,∵AP=20×1=20,
∴(4k)2+($\frac{16}{3}$k)2=202,
∴k=3,
∴AB=7,PB=15,
∴乙从A到B的运动时间=$\frac{7}{3.5}$=2s,从B到P的运动时间=22-2=20s,
∴乙的游泳速度为$\frac{15}{20}$=0.75米/秒.
点评 本题考查解直角三角形的应用、锐角三角函数、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{{{({-2})}^2}}=-2$ | B. | $\sqrt{{{({-3})}^2}}=9$ | C. | $\sqrt{x^2}=x$ | D. | $\sqrt{{{({-5})}^2}}=5$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:
在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:| 组别 | 步数分组 | 频数 |
| A | 5500≤x<6500 | 2 |
| B | 6500≤x<7500 | 10 |
| C | 7500≤x<8500 | m |
| D | 8500≤x<9500 | 3 |
| E | 9500≤x<10500 | n |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
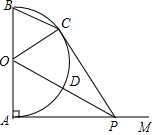 如图,AB是半圆O的直径,射线AM⊥AB,点P在AM上,连接OP交半圆O于点D,PC切半圆O于点C,连接BC,OC.
如图,AB是半圆O的直径,射线AM⊥AB,点P在AM上,连接OP交半圆O于点D,PC切半圆O于点C,连接BC,OC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com