
【题目】如图,在Rt△ABC,∠ABC=90°,AB=20,BC=15,点D为AC边上的动点,点D从点C出发,沿CA往A运动,当运动到点A时停止.若设点D的运动时间为t秒,点D运动的速度为每秒2个单位长度.
(1)当t=2时,求CD、AD的长;
(2)在D运动过程中,△CBD能否为直角三角形,若不能,请说明理由,若能,请求出t的值;
(3)当t为何值时,△CBD是等腰三角形,请直接写出t的值.

【答案】(1)CD=4,AD=21;(2)t= 4.5 或12.5秒;(3)t=6.25或7.5或9秒时,△CBD是等腰三角形.
【解析】试题分析:(1)根据CD=速度×时间列式计算即可得解,利用勾股定理列式求出AC,再根据AD=AC-CD代入数据进行计算即可得解;
(2)分①∠CDB=90°时,利用△ABC的面积列式计算即可求出BD,然后利用勾股定理列式求解得到CD,再根据时间=路程÷速度计算;②∠CBD=90°时,点D和点A重合,然后根据时间=路程÷速度计算即可得解;
(3)分①CD=BD时,过点D作DE⊥BC于E,根据等腰三角形三线合一的性质可得CE=BE,从而得到CD=AD;②CD=BC时,CD=6;③BD=BC时,过点B作BF⊥AC于F,根据等腰三角形三线合一的性质可得CD=2CF,再由(2)的结论解答.
试题解析:(1) t=2时,CD=2×2=4
∵∠ABC=90°,AB=20,BC=15
∴AC=![]()
AD=AC-CD=25-4=21
(2) ① ∠CDB=90°时, ![]()
即![]()
解得BD=12
所以CD=![]()
t= 9÷2=4.5
②∠CBD=90°时,点D和点A重合
t=25÷2=12.5
综上所述,t= 4.5 或12.5秒
(3)①CD=BD时,如图1,过点D作DE⊥BC于E,

则CE=BE,
CD=AD=![]() AC=
AC=![]() ×25=12.5,
×25=12.5,
t=12.5÷2=6.25;
②CD=BC时,CD=15,t=15÷2=7.5;
③BD=BC时,如图2,过点B作BF⊥AC于F,
则CF=9,
CD=2CF=9×2=18,
t=18÷2=9,
综上所述,t=6.25或7.5或9秒时,△CBD是等腰三角形.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】如图,已知直线l1∥l2,A,B分别是l1,l2上的点,l3和l1,l2分别交于点C,D,P是线段CD上的动点(点P不与C,D重合).
(1)若∠1=150°,∠2=45°,求∠3的度数;
(2)若∠1=α,∠2=β,用α,β表示∠APC+∠BPD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AC∥BD,AO、BO分别是∠BAC、∠ABD的平分线,那么下列结论错误的是( ) 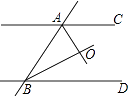
A.∠BAO与∠CAO相等
B.∠BAC与∠ABD互补
C.∠BAO与∠ABO互余
D.∠ABO与∠DBO不等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将坐标原点O沿x轴向左平移2个单位长度得到点A,过点A作y轴的平行线交反比例函数![]() 的图象于点B,AB=
的图象于点B,AB=![]() .
.
(1)求反比例函数的解析式;
(2)若P(![]() ,
, ![]() )、Q(
)、Q(![]() ,
, ![]() )是该反比例函数图象上的两点,且
)是该反比例函数图象上的两点,且![]() 时,
时, ![]() ,指出点P、Q各位于哪个象限?并简要说明理由.
,指出点P、Q各位于哪个象限?并简要说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是直线AB上一点,OC平分∠AOB,在直线AB另一侧,以O为顶点作∠DOE=90°.
(1)若∠AOE=48°,则∠BOD=______,∠AOE与∠BOD的关系是_______;
(2)∠AOE与∠COD有什么关系?请写出你的结论,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个面积为1的正方形,经过一次“生长”后,在它的左右肩上生出两个小正方形(如图1),其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,生出了4个正方形(如图2),如果按此规律继续“生长”下去,它将变得“枝繁叶茂”.在“生长”了2 017次后形成的图形中所有正方形的面积和是( )
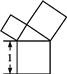

图1 图2
A. 2015 B. 2016 C. 2017 D. 2018
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将6张小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.当AB长度不变而BC变长时,将6张小长方形纸片还按照同样的方式放在新的长方形ABCD内,S1与S2的差总保持不变,则a,b满足的关系是

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD是⊙O的内接正方形,延长BA到E,使AE=AB,连接ED.
(1)求证:直线ED是⊙O的切线;
(2)连接EO交AD于点F,求证:EF=2FO.
查看答案和解析>>
科目:初中数学 来源: 题型:
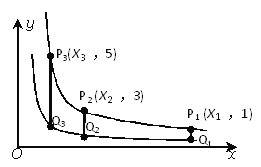
【题目】如图,函数y=![]() 和y=
和y=![]() 在第一象限的图像,点P1,P2,P3,……,P2011都是曲线上的点,它们的横坐标分别为x1,x2,x3,……,x2011,纵坐标分别为1,3,5,7……,是连续的2011个奇数,过各个P点作y的平行线,与另一双曲线交点分别是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),……,Q2012(x2012,y2012),则y2012=___________
在第一象限的图像,点P1,P2,P3,……,P2011都是曲线上的点,它们的横坐标分别为x1,x2,x3,……,x2011,纵坐标分别为1,3,5,7……,是连续的2011个奇数,过各个P点作y的平行线,与另一双曲线交点分别是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),……,Q2012(x2012,y2012),则y2012=___________
【答案】![]()
【解析】由题意得,P2012(x2012,4023),因为点P2012在y=![]() 的图象上,所以x2012=
的图象上,所以x2012=![]() ,把x2012=
,把x2012=![]() 代入 y=
代入 y=![]() 中得y2012=
中得y2012=![]() =
=![]() ,故答案为
,故答案为![]() .
.
【题型】填空题
【结束】
17
【题目】已知y是x的反比例函数,且当x=-4时,y=![]() ,
,
(1)求这个反比例函数关系式和自变量x的取值范围;
(2)求当x=6时函数y的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com