练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．当m=-9时，关于x的方程x2-6x-m=0有两个相等的实数根．

    分析 由方程有两根相等的实数根结合根的判别式，即可得出关于m的一元一次方程，解方程即可得出结论．

    解答 解：∵关于x的方程x2-6x-m=0有两个相等的实数根，
    ∴△=（-6）2-4×1×（-m）=36+4m=0，
    解得：m=-9．
    故答案为：-9．

    点评 本题考查了根的判别式，解题的关键是得出△=36+4m=0．本题属于基础题，难度不大，解决该题型题目时，根据方程根的情况结合根的判别式，得出方程（不等式或不等式组）关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    19．网络时代的到来，很多家庭都接入了网络，电信局规定了拨号入网两种收费方式，用户可以任选其一；
    ①某用户某月上网的时间为x小时，两种收费方式的费用分别为yA（元）、yB（元）．写出yA、yB与x之间的函数关系式；
    ②在上网时间相同的条件下，请你帮该用户选择哪种方式上网更省钱？
    月租费（元）计费方式（元/分）
    A方式00.05
    B方式540.02

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如图，在△ABC中，AB=AC，作AD⊥AB交BC的延长线于点D，作AE∥BD，CE⊥AC，且AE，CE相交于点E，求证：AD=CE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．计算：$\sqrt{8a}÷\sqrt{2a}$=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．下列各式计算正确的是（　　）
    A．$\sqrt{2}+\sqrt{3}=\sqrt{5}$B．$2+\sqrt{2}=2\sqrt{2}$C．$3\sqrt{2}-\sqrt{2}=2\sqrt{2}$D．$\frac{{\sqrt{12}+\sqrt{10}}}{2}=\sqrt{6}+\sqrt{5}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．如图，在△ABC中，AD为BC边上的中线，E为AC上的一点，BE交AD于点F，已知AE=EF．求证：AC=BF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．为了改善办学条件，学校购置了笔记本电脑和台式电脑共100台，已知笔记本电脑的台数比台式电脑的台数的$\frac{1}{4}$还少5台，则购置的笔记本电脑有16台．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

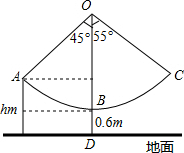    18．某新农村乐园设置了一个秋千场所，如图所示，秋千拉绳OB的长为3m，静止时，踏板到地面距离BD的长为0.6m（踏板厚度忽略不计）．为安全起见，乐园管理处规定：儿童的“安全高度”为hm，成人的“安全高度”为2m（计算结果精确到0.1m）
    （1）当摆绳OA与OB成45°夹角时，恰为儿童的安全高度，则h=1.5m
    （2）某成人在玩秋千时，摆绳OC与OB的最大夹角为55°，问此人是否安全？（参考数据：$\sqrt{2}$≈1.41，sin55°≈0.82，cos55°≈0.57，tan55°≈1.43）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

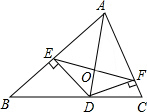    11．如图，在△ABC中，AB=c，AC=b．AD是△ABC的角平分线，DE⊥A于E，DF⊥AC于F，EF与AD相交于O，已知△ADC的面积为1．
    （1）证明：DE=DF；
    （2）试探究线段EF和AD是否垂直？并说明理由；
    （3）若△BDE的面积是△CDF的面积2倍．试求四边形AEDF的面积．

    查看答案和解析>>

    同步练习册答案