
【题目】已知关于x的一元二次方程![]() 有实数根.
有实数根.
(1)求k的取值范围;
(2)若k为正整数,且方程有两个非零的整数根,求k的取值.
【答案】(1)![]() ;(2)k=3
;(2)k=3
【解析】
(1)根据一元二次方程2x2+4x+k﹣1=0有实数根,可得出△≥0,解不等式即可得出结论;
(2)分别把k的正整数值代入方程2x2+4x+k﹣1=0,根据解方程的结果进行分析解答.
(1)由题意得:△=16﹣8(k﹣1)≥0,∴k≤3.
(2)∵k为正整数,∴k=1,2,3.
当k=1时,方程2x2+4x+k﹣1=0变为:2x2+4x =0,解得:x=0或x=-2,有一个根为零;
当k=2时,方程2x2+4x+k﹣1=0变为:2x2+4x +1=0,解得:x=![]() ,无整数根;
,无整数根;
当k=3时,方程2x2+4x+k﹣1=0变为:2x2+4x +2=0,解得:x1=x2=-1,有两个非零的整数根.
综上所述:k=3.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=![]() AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )
AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )

A. ①② B. ②③ C. ①③ D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张正面分别标有数字﹣1,2,﹣3,4的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上洗均匀.
(1)随机抽取一张卡片,求抽到标有负数的卡片的概率;
(2)设平面直角坐标系内点A(x,y),现随机抽取一张卡片,将卡片上的数字记作x,然后不放回,再随机抽取一张卡片,将卡片上的数字记作y.请求出点A在第二象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
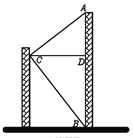
【题目】小明家所在居民楼的对面有一座大厦AB=74米,为测量这座居民楼与大厦之间的水平距离CD的长度,小明从自己家的窗户C处测得∠DCA=37°,∠DCB=48°(DC平行于地面).求小明家所在居民楼与大厦的距离CD的长度.
(参考数据:sin37°![]() ,tan37°
,tan37°![]() ,sin48°
,sin48°![]() ,tan48°
,tan48°![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,点
中,点![]() 是线段
是线段![]() 上一动点,
上一动点, ![]() 为
为![]() 的中点,
的中点, ![]() 的延长线交BC于
的延长线交BC于![]() .
.
(1)求证: ![]() ;
;
(2)若![]() ,
,![]() ,
,![]() 从点
从点![]() 出发,以l
出发,以l![]() 的速度向
的速度向![]() 运动(不与
运动(不与![]() 重合).设点
重合).设点![]() 运动时间为
运动时间为![]() ,请用
,请用![]() 表示
表示![]() 的长;并求
的长;并求![]() 为何值时,四边形
为何值时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
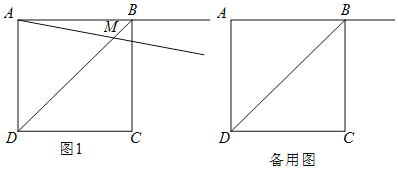
【题目】正方形ABCD的边长为2,将射线AB绕点A顺时针旋转α,所得射线与线段BD交于点M,作CE⊥AM于点E,点N与点M关于直线CE对称,连接CN.
(1)如图,当0°<α<45°时:
①依题意补全图;
②用等式表示∠NCE与∠BAM之间的数量关系:___________;
(2)当45°<α<90°时,探究∠NCE与∠BAM之间的数量关系并加以证明;
(3)当0°<α<90°时,若边AD的中点为F,直接写出线段EF长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量![]() (件
(件![]() 与销售价
与销售价![]() (元/件)之间的函数关系如图所示.
(元/件)之间的函数关系如图所示.
(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)求每天的销售利润W(元![]() 与销售价
与销售价![]() (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,点E为边AB上一动点,连结CE并将其绕点C顺时针旋转90°得到CF,连结DF,以CE、CF为邻边作矩形CFGE,GE与AD、AC分别交于点H、M,GF交CD延长线于点N.
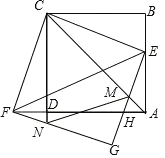
(1)证明:点A、D、F在同一条直线上;
(2)随着点E的移动,线段DH是否有最小值?若有,求出最小值;若没有,请说明理由;
(3)连结EF、MN,当MN∥EF时,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
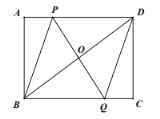
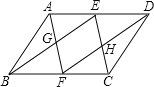
【题目】如图,在平行四边形ABCD中,E、F分别是AD、BC的中点,连接AF、BE交于点G,连接CE、DF交于点H.
(1)求证:四边形EGFH为平行四边形;
(2)当AB与BC满足什么条件时,四边形EGFH为矩形?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com