
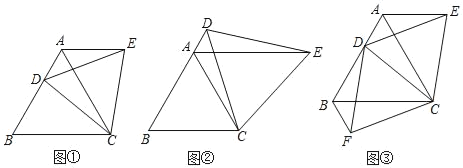
【题目】(1)操作发现:如图①,点D是等边△ABC的边AB上一动点(点D与点B不重合),连接CD,以CD为边在CD上方作等边△CDE,连接AE,则AE与BD有怎样的数量关系?说明理由.
(2)类比猜想:如图②,若点D是等边△ABC的边BA延长线上一动点,连接CD,以CD为边在CD上方作等边△CDE,连接AE,请直接写出AE与BD满足的数量关系,不必说明理由;
(3)深入探究:如图③,点D是等边△ABC的边AB上一动点(点D与点B不重合),连接CD,以CD为边分别在CD上方、下方作等边△CDE和等边△CDF,连接AE,BF则AE,BF与AB有怎样的数量关系?说明理由.
【答案】(1)AE=BD;(2)AE=BD;(3)AE+BF=AB.
【解析】
(1)根据等边三角形的三条边、三个内角都相等的性质,利用全等三角形的判定定理SAS可以证得△BCD≌△ACE;然后由全等三角形的对应边相等知AE=BD
(2)通过证明△BCD≌△ACE,即可证明AE=BD;
(3)1.AF+BF=AB;利用全等三角形△BCD≌△ACE(SAS)的对应边BD=AE;同理△BCF≌△DCA (SAS),则BF=AD,所以AE+BF =AB
解:(1)AE=BD,理由如下:
∵△ABC和△DCE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB﹣∠ACD=∠DCE﹣∠ACD,
即∠BCD=∠ACE,
在△BCD和△ACE中,
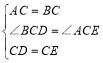 ,
,
∴△BCD≌△ACE(SAS),
∴AE=BD;
(2)AE=BD.
理由如下:∵△ABC和△DCE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠ACD=∠DCE+∠ACD,
即∠BCD=∠ACE,
在△BCD和△ACE中,
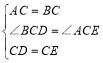 ,
,
∴△BCD≌△ACE(SAS),
∴AE=BD;
(3)AE+BF=AB.
证明如下:由(1)知,△BCD≌△ACE(SAS),
∴BD=AE,
同理可证,△BCF≌△DCA(SAS),
∴BF=AD,
∴AB=AD+BD=AE+BF.


 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】我们约定,在平面直角坐标系![]() 中,经过象限内某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“参照线”.例如,点
中,经过象限内某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“参照线”.例如,点![]() 的参照线有:
的参照线有:![]() ,
,![]() ,
,![]() ,
,![]() (如图1).
(如图1).
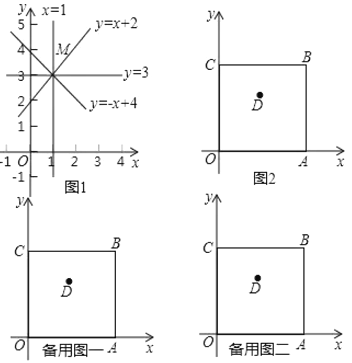
如图2,正方形![]() 在平面直角坐标系
在平面直角坐标系![]() 中,点
中,点![]() 在第一象限,点
在第一象限,点![]() ,
,![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,点
轴上,点![]() 在正方形内部.
在正方形内部.
(1)直接写出点![]() 的所有参照线: ;
的所有参照线: ;
(2)若![]() ,点
,点![]() 在线段
在线段![]() 的垂直平分线上,且点
的垂直平分线上,且点![]() 有一条参照线是
有一条参照线是![]() ,则点
,则点![]() 的坐标是_______________;
的坐标是_______________;
(3)在(2)的条件下,点![]() 是
是![]() 边上任意一点(点
边上任意一点(点![]() 不与点
不与点![]() ,
,![]() 重合),连接
重合),连接![]() ,将
,将![]() 沿着
沿着![]() 折叠,点
折叠,点![]() 的对应点记为
的对应点记为![]() .当点
.当点![]() 在点
在点![]() 的平行于坐标轴的参照线上时,写出相应的折痕
的平行于坐标轴的参照线上时,写出相应的折痕![]() 所在直线的解析式: .
所在直线的解析式: .
查看答案和解析>>
科目:初中数学 来源: 题型:
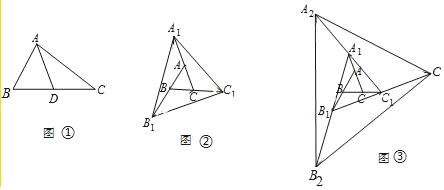
【题目】如图①,△ABC中,AD为BC边上的中线,则有S△ABD=S△ACD,许多面积问题可以转化为这个基本模型解答.如图②,已知△ABC的面积为1,把△ABC各边均顺次延长一倍,连结所得端点,得到△A1B1C1,即将△ABC向外扩展了一次,则扩展一次后的△A1B1C1的面积是_____,如图③,将△ABC向外扩展了两次得到△A2B2C2,……,若将△ABC向外扩展了n次得到△AnBnn,则扩展n次后得到的△AnBnn面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的顶点为D.
的顶点为D.
(1)求点D的坐标(用含m的代数式表示);
(2)若该抛物线经过点A(1,m),求m的值;
(3)在(2)的条件下,抛物线与x轴是否有交点,若有,求出交点坐标,若没有,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A ,D,B,E在同一条直线上,且AD = BE, AC = DF,补充下列其中一个条件后,不一定能得到△ABC≌△DEF 的是( )

A.BC = EFB.AC//DFC.∠C = ∠FD.∠BAC = ∠EDF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县为落实“精准扶贫惠民政策”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合作施工15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙两队合作完成.则甲、乙两队合作完成该工程需要多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班将举行“数学知识竞赛”活动,班长安排小明购买奖品,下面两图是小明买回奖品时与班长的对话情境:

请根据上面的信息,解决问题:
(1)试计算两种笔记本各买了多少本?
(2)请你解释:小明为什么不可能找回68元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com