练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    8．先化简，再求值：$\frac{（1+x）^{2}}{1-{x}^{2}}$÷（$\frac{2x}{1-x}$-x），其中x=$\sqrt{5}$-2．

    分析 先根据分式混合运算的法则把原式进行化简，再把x的值，代入原式进行计算即可．

    解答 解：原式=$\frac{（1+x）^{2}}{（1+x）（1-x）}$÷$\frac{2x-x+{x}^{2}}{1-x}$=$\frac{（1+x）^{2}}{（1+x）（1-x）}$•$\frac{1-x}{x（1+x）}$=$\frac{1}{x}$，
    当x=$\sqrt{5}$-2时，$\frac{1}{x}$=$\frac{1}{\sqrt{5}-2}$=$\frac{\sqrt{5}+2}{（\sqrt{5}-2）（\sqrt{5}+2）}$=$\sqrt{5}$+2．

    点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    9．如图，平行四边形ABCD对角线相交于点O，M是AD的中点，连结CM，交BD于点N．则S△AOB：S△CON：S△DMN=3：1：1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．掷两枚般子，请你分别写出一个必然事件：点数不小于2；一个不可能事件：点数大于12；一个随机事件：点数是6．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

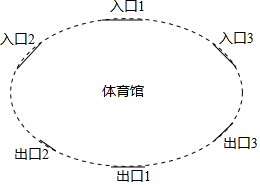    16．某体育馆有3个入口和3个出口，其示意图如下，参观者可从任意一个入口进入，参观结束后从任意一个出口离开
    （1）用树状图表示，小明从进入到离开，对于入口和出口的选择共有多少种不同的结果？
    （2）小明从入口1进入并从出口2离开的概率是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．计算：（-3）0+（$\frac{1}{2}$）-1-8×$\frac{\sqrt{2}}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．已知点P和点Q在数轴上的位置如图，设点P，Q，N对应的实数分别为p，q，n，且pq=n，则点N作数轴上的位置可能是（　　）
    A．B．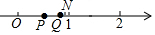
    C．D．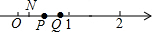

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．阅读下列材料，完成相应任务：
    折纸三等分角
         三等分角问题（trisection of an angle）是二千四百年前，古希腊人提出的几何三大作图问题之一（三等分任意角、化圆为方、倍立方），即用圆规与直尺（没有刻度，只能做直线的尺子）把一任意角三等分，这问题曾吸引着许多人去研究，但无一成功．1837年法国数学家凡齐尔（1814～1848）运用代数方法证明了，仅用尺规不可鞥呢三等分角．
         如果作图工具没有限制，将条件放宽，将任意角三等分是可以解决的．下面介绍一种折纸三等分任意锐角的方法：
        （1）在正方形纸片上折出任意∠SBC，将正方形ABCD对折，折痕为记为MN，再将矩形MBCN对折，折痕记为EF，得到图（1）；
        （2）翻折左下角使点B与EF上的点T重合，点M与SB上的点P重合，点E对折后的对应点记为Q，折痕为记为GH，得到图（2）；
        （3）折出射线BQ，BT，得到图（3），则射线BQ，BT就是∠SBC的三等分线．
    下面是证明BQ，BT是∠SBC三等分线的部分过程：
    证明：过T作TK⊥BC，垂足为K，则四边形EBKT为矩形
    根据折叠，得EB=QT，∠EBT=∠QTB，BT=TB
    ∴△EBT≌△QTB，
    ∴∠BQT=∠TEB=90°，
    ∴BQ⊥PT
    …
    学习任务：
    （1）将剩余部分的证明过程补充完整；
    （2）若将图（1）中的点S与点D重合，重复材料中的操作过程得到图（4），请利用图（4），直接写出tan15°=2-$\sqrt{3}$（不必化简）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．已知：线段AB⊥BM，垂足为B，点O和点A在直线BM的同侧，且tan∠OBM=2，AB=5，设以O为圆心，BO为半径的圆O与直线BM的另一个交点为C，直线AO与直线BM的交点为D，圆O为直线AD的交点为E．
    （1）如图1，当点D在BC的延长线上时，设BC=x，CD=y，求y关于x的函数解析式，并写出定义域．
    （2）在（1）的条件下，当BC=CE时，求BC的长；
    （3）当△ABO是以AO为腰的等腰三角形时，求∠ADB的正切值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．如图，平行四边形ABCD中，AC与BD相交于点O，AB=AC，延长BC到点E，使CE=BC，连接AE，分别交BD、CD于点F、G．
    （1）求证：△ADB≌△CEA；
    （2）若BD=9，求AF的长．

    查看答案和解析>>

    同步练习册答案