练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
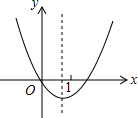
    20．已知抛物线y=ax2+bx+c的图象如图所示，则|a-b+c|+|2a+b|=（　　）
    A．a+bB．a-2bC．a-bD．3a

    分析 观察函数图象找出“a＞0，c=0，-2a＜b＜0”，由此即可得出|a-b+c|=a-b，|2a+b|=2a+b，根据整式的加减法运算即可得出结论．

    解答 解：观察函数图象，发现：
    图象过原点，c=0；
    抛物线开口向上，a＞0；
    抛物线的对称轴0＜-$\frac{b}{2a}$＜1，-2a＜b＜0．
    ∴|a-b+c|=a-b，|2a+b|=2a+b，
    ∴|a-b+c|+|2a+b|=a-b+2a+b=3a．
    故选D．

    点评 本题考查了二次函数图象与系数的关系，解题的关键是找出|a-b+c|=a-b，|2a+b|=2a+b．本题属于基础题，难度不大，解决该题型题目时，根据二次函数的图象找出系数间的关系是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    10．如图，∠AOB=30°，点M、N分别在边OA、OB上，且OM=2，ON=6，点P、Q分别在边OB、OA上，则MP+PQ+QN的最小值是（　　）
    A．2$\sqrt{10}$B．$\sqrt{10}$C．20D．2$\sqrt{5}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．在△ABC中，D，E分別是AB，AC的中点，AC=10．F是DE上一点．连接AF，CF，DF=1，若∠AFC=90°，则BC的长度为12．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．把（-6）+（+3）-（-1）+（-2）写成省略加号和的形式是-6+3+1-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．在一次中学生趣味数学竞赛中，参加比赛的10名学生的成绩如下表所示：
    分数80859095
    人数1432
    这10名学生所得分数的平均数是（　　）
    A．86B．88C．90D．92

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．计算
    （1）$\frac{2x}{x+1}+\frac{2}{x+1}$
    （2）a-1-$\frac{{a}^{2}}{a+1}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．4的平方根是（　　）
    A．16B．±16C．2D．±2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

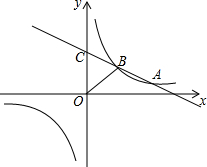    9．如图，一次函数y=kx+b（k＜0）与反比例函数y=$\frac{m}{x}$的图象相交于A、B两点，一次函数的图象与y轴相交于点C，已知点A（4，1）
    （1）求反比例函数的解析式；
    （2）连接OB（O是坐标原点），若△BOC的面积为3，求该一次函数的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．分式方程$\frac{4}{x}$=$\frac{3}{x-1}$的解是x=4．

    查看答案和解析>>

    同步练习册答案