
【题目】现有一块直角三角形的铁皮![]() ,
,![]() ,
,![]() ,
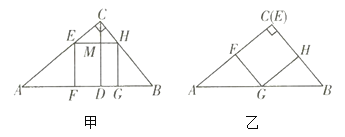
,![]() .要在其中剪出一个面积尽可能大的正方形,小红和小亮各想出了甲、乙两种方案,请你帮忙算一算哪一种方案剪出的正方形面积较大?
.要在其中剪出一个面积尽可能大的正方形,小红和小亮各想出了甲、乙两种方案,请你帮忙算一算哪一种方案剪出的正方形面积较大?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】对于任意一个自然数N,将其各个数位上的数字相加得到一个数,我们把这一过程称为一次操作,把这个得到的数进行同样的操作,不断进行下去,最终会得到一个一位数K,我们把K称为N的“终极数”,并记f(N)=K.例如,456→4+5+6=15→1+5=6,∴f(456)=6.
(1)计算:f(2019)= .f(20192020)= .
(2)有一个三位自然数M=![]() ,已知f(M)=4,且x<y<z,请求出所有满足条件的自然数M.
,已知f(M)=4,且x<y<z,请求出所有满足条件的自然数M.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,∠D=45°,∠BAC=90°,点E为BC边上一点,将AE绕点A按顺时针方向旋转90°后能与AF重合,且FB⊥BC,点G是FB与AE的交点,点E是AG的中点.
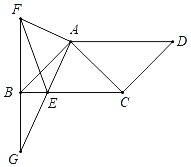
(1)若AG=2![]() ,BE=1,求BF的长;
,BE=1,求BF的长;
(2)求证:![]() AB=BG+2BE.
AB=BG+2BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级数学兴趣小组在研究相似多边形问题时,他们提出了两个观点:
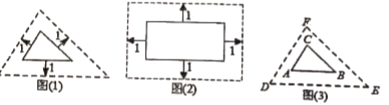
观点一:将外面大三角形按图1的方式向内缩小,得到新三角形,它们的对应边间距都为1,则新三角形与原三角形相似.
观点二:将邻边为6和10的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距都为1,则新矩形与原矩形相似.
请回答下列问题:
(1)你认为上述两个观点是否正确,说明理由.
(2)如图3,若![]() 的周长和面积都是24,
的周长和面积都是24,![]() ,将
,将![]() 按图3的方式向外扩张,得到
按图3的方式向外扩张,得到![]() ,它们的对应边间距都为
,它们的对应边间距都为![]() ,
,![]() ,求
,求![]() 的周长和面积.
的周长和面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
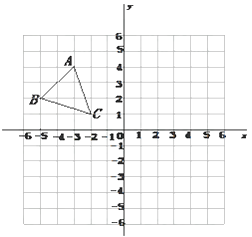
【题目】如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC 的三个顶点的坐标分别 A(-3,4)B(-5,2)C(-2,1)
(1)画出 △ABC关于y 轴的对称图形 △A1B1C1;
(2)画出将△ABC 绕原点 O逆时针方向旋转90°得到的△A2B2C2 ;
(3)求(2)中线段 OA扫过的图形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要建一个长方形养鸡场,鸡场的一边靠墙,如果用50m长的篱笆围成中间有一道篱笆隔墙的养鸡场,设它的长度为x m.
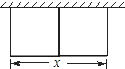
(1)要使鸡场面积最大,鸡场的长度应为多少m?
(2)如果中间有n(n是大于1的整数)道篱笆隔墙,要使鸡场面积最大,鸡场的长应为多少m?
比较(1)(2)的结果,你能得到什么结论?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某乡镇在“精准扶贫”活动中销售一农产品,经分析发现月销售量y(万件)与月份x(月)的关系为:![]() ,每件产品的利润z(元)与月份x(月)的关系如下表:
,每件产品的利润z(元)与月份x(月)的关系如下表:
x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
z | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 10 | 10 |
(1)请你根据表格求出每件产品利润z(元)与月份x(月)的关系式;
(2)若月利润w(万元)=当月销售量y(万件)×当月每件产品的利润z(元),求月利润w(万元)与月份x(月)的关系式;
(3)当x为何值时,月利润w有最大值,最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
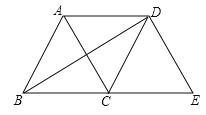
【题目】如图,等边![]() 沿射线
沿射线![]() 向右平移到
向右平移到![]() 的位置,连接
的位置,连接![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() 互相平分;③四边形
互相平分;③四边形![]() 是菱形;④
是菱形;④![]() 。其中正确的个数是( )
。其中正确的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com