
 几何计算题:
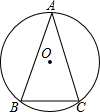
几何计算题:分析 (1)根据同圆或等圆中等弧所对圆周角相等,得出∠B=∠C=75°,再利用三角形内角和定理求出即可;
(2)作OE⊥AB于E,OF⊥CD于F,连OA,OC,由垂径定理得AE=$\frac{1}{2}$AB=5,CF=$\frac{1}{2}$CD=12,由于AB∥CD,易得E、O、F三点共线,在Rt△AOE和Rt△OCF中,利用勾股定理分别计算出OE与OF,然后讨论:当圆心O在弦AB与CD之间时,AB与CD的距离=OE+OF;当圆心O在弦A′B′与CD的外部时,AB与CD的距离=OE-OF;
(3)设三个圆的半径分别为xcm,ycm,zcm,根据已知条件可得:$\left\{\begin{array}{l}{x+y=5}\\{y+z=12}\\{z+x=13}\end{array}\right.$,解之即可得出答案.
解答 解:(1)∵⊙O中,$\widehat{AB}=\widehat{AC}$,∠C=75°,
∴AB=AC,
∴∠B=∠C=75°,
∴∠A=180°-75°×2=30°;
(2)如图作OE⊥AB于E,OF⊥CD于F,连OA,OC,OA=OC=13,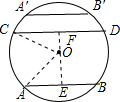
则AE=$\frac{1}{2}$AB=5,CF=$\frac{1}{2}$CD=12,
∵AB∥CD,
∴E、O、F三点共线,
在Rt△COF中,OF=$\sqrt{O{C}^{2}-C{F}^{2}}$=$\sqrt{1{3}^{2}-1{2}^{2}}$=5,
在Rt△AOE中,OE=$\sqrt{O{A}^{2}-A{E}^{2}}$=$\sqrt{1{3}^{2}-{5}^{2}}$=12,
当圆心O在弦AB与CD之间时,AB与CD的距离=OE+OF=12+5=17;
当圆心O在弦A′B′与CD的外部时,AB与CD的距离=OE-OF=12-5=7.
所以AB与CD的距离是17或7;
(3)解:设三个圆的半径分别为xcm,ycm,zcm,
由于三角形三边长分别为5cm,12cm,13cm,得到这个三角形三个顶点为圆心的三个圆两两外切,
那么容易列方程得:$\left\{\begin{array}{l}{x+y=5}\\{y+z=12}\\{z+x=13}\end{array}\right.$,
①-②得:x-z=-7④,
③+④得2x=6,解得:x=3,
将x=3代入①得:y=2,
将y=2代入②得:z=10,
解得:$\left\{\begin{array}{l}{x=3}\\{y=2}\\{z=10}\end{array}\right.$.
故三个圆的半径分别是3cm,2cm,10cm.
点评 此题主要考查了三角形的内角和定理以及圆心角、弧、弦之间的关系等知识,根据已得出∠B=∠C=75°是解决问题的关键.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:解答题
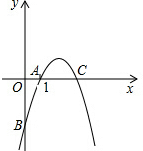 如图,抛物线y=-x2+5x+n经过点A(1,0),与x轴交于A、C两点,与y轴交于点B.
如图,抛物线y=-x2+5x+n经过点A(1,0),与x轴交于A、C两点,与y轴交于点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
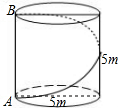 壁虎在一座油罐的下底边沿A处.它发现在自己的正上方──油罐上边缘的B处有一只害虫.壁虎决定捕捉这只害虫.为了不引起害虫的注意,它故意不走直线,而是绕着油罐,沿着一条螺旋路线,从背后对害虫进行突然袭击如图.结果,壁虎的偷袭得到成功,获得了一顿美餐.请问:壁虎沿着螺旋线爬行是最短的路程吗(线段AB除外)?
壁虎在一座油罐的下底边沿A处.它发现在自己的正上方──油罐上边缘的B处有一只害虫.壁虎决定捕捉这只害虫.为了不引起害虫的注意,它故意不走直线,而是绕着油罐,沿着一条螺旋路线,从背后对害虫进行突然袭击如图.结果,壁虎的偷袭得到成功,获得了一顿美餐.请问:壁虎沿着螺旋线爬行是最短的路程吗(线段AB除外)?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com