
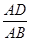 的值.
的值.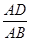 的值.
的值. (3)
(3)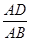 =
=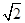
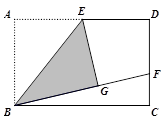
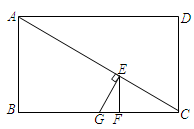
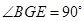 ;矩形ABCD中,E是AD的中点,所以EG=ED,
;矩形ABCD中,E是AD的中点,所以EG=ED,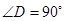 ;又因为EF是
;又因为EF是 的公共边,且是斜边,所以Rt△EGF≌ Rt△EDF,所以GF = DF.
的公共边,且是斜边,所以Rt△EGF≌ Rt△EDF,所以GF = DF.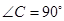 ;将△ABE沿BE折叠后得到△GBE,△ABE
;将△ABE沿BE折叠后得到△GBE,△ABE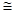 △GBE,AB=BG=9;由(1)知证明 Rt△EGF≌ Rt△EDF得GF = DF,GF=4;所以BF=BG+GE=9+4=13;CF=CD-DF=9-4=5;在Rt△BFC中由勾股定理得BC=
△GBE,AB=BG=9;由(1)知证明 Rt△EGF≌ Rt△EDF得GF = DF,GF=4;所以BF=BG+GE=9+4=13;CF=CD-DF=9-4=5;在Rt△BFC中由勾股定理得BC=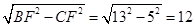 ,所以
,所以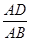 =
=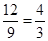
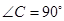 ;将△ABE沿BE折叠后得到△GBE,△ABE
;将△ABE沿BE折叠后得到△GBE,△ABE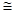 △GBE,AB=BG
△GBE,AB=BG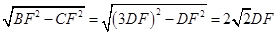 ,所以
,所以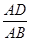 =
=


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:解答题
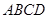 中,
中,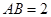 ,
,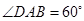 ,点
,点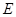 是
是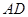 边的中点,点
边的中点,点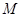 是
是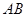 边上一动点(不与点
边上一动点(不与点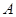 重合),延长
重合),延长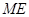 交射线
交射线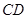 于点
于点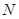 ,连接
,连接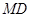 ,
,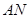 .
.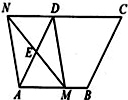
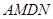 是平行四边形;
是平行四边形;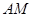 的值为 时,四边形
的值为 时,四边形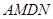 是矩形;
是矩形;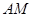 的值为 时,四边形
的值为 时,四边形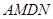 是菱形.
是菱形.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
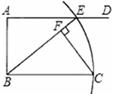
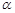 (
(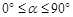 ),∠GEF的两边分别交矩形的边于点M,点N.当△MEN为等腰三角形时,求此时△MEN的面积.
),∠GEF的两边分别交矩形的边于点M,点N.当△MEN为等腰三角形时,求此时△MEN的面积.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
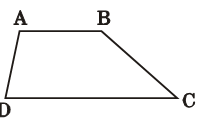
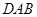 的角平分线AF和梯形的高BG(保留作图痕迹,不写作法和证明);
的角平分线AF和梯形的高BG(保留作图痕迹,不写作法和证明);查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com