
 如图,∠CAB=45°,AB=3,△ABC的面积为3,E为BC上任意一点,连AE,将△ABE,△ACE分别延AB,AC翻折至△ABM,△ACN,连MN,则MN的最小值$\frac{6}{5}$$\sqrt{10}$.
如图,∠CAB=45°,AB=3,△ABC的面积为3,E为BC上任意一点,连AE,将△ABE,△ACE分别延AB,AC翻折至△ABM,△ACN,连MN,则MN的最小值$\frac{6}{5}$$\sqrt{10}$. 分析 过C作CD⊥AB于D,根据已知条件得到CD=2,根据勾股定理得到BC=$\sqrt{B{D}^{2}+C{D}^{2}=\sqrt{5}}$,当AE⊥BC时,AE最小,根据三角形的面积公式得到AE=$\frac{2{S}_{△ABC}}{BC}$=$\frac{2×3}{\sqrt{5}}$=$\frac{6}{5}$$\sqrt{5}$,根据翻折的性质得到AM=AN=AE,根据勾股定理即可得到结论.
解答 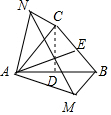 解:过C作CD⊥AB于D,
解:过C作CD⊥AB于D,
∵AB=3,△ABC的面积为3,
∴CD=2,
∵∠CAB=45°,
∴AD=CD=2,
∴BC=1,
∴BC=$\sqrt{B{D}^{2}+C{D}^{2}=\sqrt{5}}$,
∴当AE⊥BC时,AE最小,
∴AE=$\frac{2{S}_{△ABC}}{BC}$=$\frac{2×3}{\sqrt{5}}$=$\frac{6}{5}$$\sqrt{5}$,
∵将△ABE,△ACE分别延AB,AC翻折至△ABM,△ACN,
∴AM=AN=AE,
∵∠CAB=45°,
∴∠MAN=90°,
∴MN=$\sqrt{A{N}^{2}+A{M}^{2}}$=$\frac{6}{5}$$\sqrt{10}$.
故答案为:$\frac{6}{5}$$\sqrt{10}$.
点评 本题考查了翻折的性质,勾股定理,三角形的面积公式,熟练掌握折叠的性质是解题的关键.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△ABC中,AB=AC=5,BC=6,BD⊥AC于点D,将△BCD绕点B逆时针旋转,旋转角的大小与∠CBA相等,如果点C、D旋转后分别落在点E、F的位置,那么∠EFD的正切值是$\frac{1}{2}$.
如图,△ABC中,AB=AC=5,BC=6,BD⊥AC于点D,将△BCD绕点B逆时针旋转,旋转角的大小与∠CBA相等,如果点C、D旋转后分别落在点E、F的位置,那么∠EFD的正切值是$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
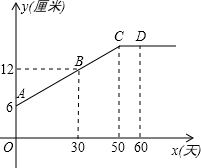 某生物小组观察一植物生长,得到植物的高度(单位:厘米)与观察时间(单位:天)的关系,并画出如下的图象(AC是线段,直线CD平行于x轴.)
某生物小组观察一植物生长,得到植物的高度(单位:厘米)与观察时间(单位:天)的关系,并画出如下的图象(AC是线段,直线CD平行于x轴.)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com