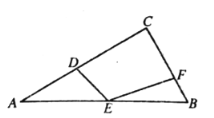
【题目】如图，在
中，
，
，点
在边
上，
，
，点
，
分别是边
，
上的动点，连接
，
，则
的最小值为_________.
【答案】
【解析】
作点D关于AB的对称点G，过点G作GF
于点F交AB于点E，此时
取得最小值. 先证出AC∥GF，得∠GEA=∠A=30
=∠DEA，可得DE=AD=4，由勾股定理求得EM的长，根据30角的直角三角形的特点以及勾股定理再求出AB，EF，即可得的值.
作点D关于AB的对称点G，过点G作GF于点F交AB于点E，此时取得最小值.
∵GF
∴∠GFB=∠C=90
∴AC∥GF
∴∠GEA=∠A=30
∴∠DEA=30
∴DE=AD=4
∴DM=2
EM=
∴AE=4
∵AC=AD+CD=4+5=9
∵ ∠A=30
∴BC=
，∠B=60
∵
∴
，
AB=
∴BE=AB-AE=
BF=
BE=，
∴EF=
=3
∴DE+EF的最小值是4+3=7.
故答案为：7.
科目：初中数学 来源： 题型：
【题目】如图1，CE平分∠ACD，AE平分∠BAC，∠EAC+∠ACE=90°
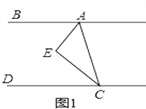
（1）请判断AB与CD的位置关系并说明理由；
（2）如图2，在（1）的结论下，当∠E=90°保持不变，移动直角顶点E，使∠MCE=∠ECD，当直角顶点E点移动时，问∠BAE与∠MCD是否存在确定的数量关系？
（3）如图3，在（1）的结论下，P为线段AC上一定点，点Q为直线CD上一动点，当点Q在射线CD上运动时（点C除外）∠CPQ+∠CQP与∠BAC有何数量关系？ （2、3小题只需选一题说明理由）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】A、B两地相距20千米，甲、乙两人都从A地去B地，图中射线l1和l2分别表示甲、乙两人所走路程s（千米）与时间t（小时）之间的关系．
下列说法：
①乙晚出发1小时；
②乙出发3小时后追上甲；
③甲的速度是4千米/小时，乙的速度是6千米/小时；
④乙先到达B地．其中正确的个数是（ ）
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某旅游商品经销店欲购进A、B两种纪念品，若用380元购进A种纪念品7件，B种纪念品8件；也可以用380元购进A种纪念品10件，B种纪念品6件．
（1）求A、B两种纪念品的进价分别为多少？
（2）若该商店每销售1件A种纪念品可获利5元，每销售1件B种纪念品可获利7元，该商店准备用不超过900元购进A、B两种纪念品40件，且这两种纪念品全部售出时总获利不低于216元，问应该怎样进货，才能使总获利最大，最大为多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在
中，
，
，点
是
的中点，点
是
上的一点（点不与点，
重合）.过点
，点作直线
的垂线，垂足分别为点
和点
.
图1. 
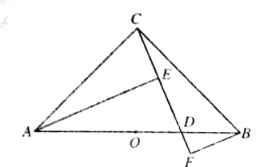图2.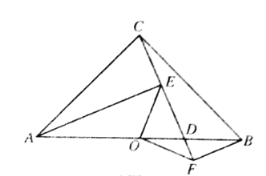 
（1）如图1，求证：
；（2）如图2，连接
，
，请判断线段与之间的数量关系和位置关系，并说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在如图所示的正方形网格中，每个小正方形的边长为1各单位，格点三角形（顶点是网格线的交点的三角形）△ABC的顶点A，B的坐标分别为（1，4），（﹣3，1）．
（1）请在网格所在的平面内作出符合上述表述的平面直角坐标系；
（2）请你将A、B、C的横坐标不变，纵坐标乘以﹣1所得到的点A1、B1、C1描在坐标系中，并画出△A1B1C1，其中点C1的坐标为 ．
（3）△ABC的面积是 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，AB=AC，以AC为直径的⊙O与边AB，BC分别交于点D，E．过E的直线与⊙O相切，与AC的延长线交于点G，与AB交于点F．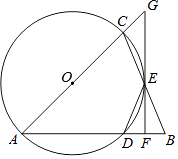
（1）求证：△BDE为等腰三角形；
（2）求证：GF⊥AB；
（3）若⊙O半径为3，DF=1，求CG的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】计算题
（1）若a=cos45°，b=（π+1）0 ， c= 
，d=（﹣ 
）﹣1 ， 化简得
a= ， b= ， c= ， d=；
（2）在（1）的条件下，试计算 
﹣cd．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
