练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．计算：$\sqrt{12}$+|$\sqrt{3}$-3|-2sin60°-（$\sqrt{3}$）2+20160．

    分析 原式利用二次根式性质，绝对值的代数意义，零指数幂法则，以及平方根定义计算即可得到结果．

    解答 解：原式=2$\sqrt{3}$+3-$\sqrt{3}$-$\sqrt{3}$-3+1=1．

    点评 此题考查了实数的运算，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    12．如图是一个半圆形桥洞截面示意图，圆心为O，直径AB是河底线，弦CD是水位线，CD∥AB，且CD=24 m，OE⊥CD于点E．已测得sin∠DOE=$\frac{12}{13}$．
    （1）求AB的长；
    （2）根据需要，水面要以每小时0.5m的速度下降，则经过多长时间才能将水排干？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．类似于平面直角坐标系，如图1，在平面内，如果原点重合的两条数轴不垂直，那么我们称这样的坐标系为斜坐标系．若P是斜坐标系xOy中的任意一点，过点P分别作两坐标轴的平行线，与x轴、y轴交于点M、N，如果M、N在x轴、y轴上分别对应的实数是a、b，这时点P的坐标为（a，b）．
    （1）如图2，在斜坐标系xOy中，画出点A（-2，3）；
    （2）如图3，在斜坐标系xOy中，已知点B（5，0）、C（0，4），且P（x，y）是线段CB上的任意一点，则y与x之间的等量关系式为y=-$\frac{4}{5}$x+4；
    （3）若（2）中的点P在线段CB的延长线上，其它条件都不变，试判断（2）中的结论是否仍然成立，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．计算
    （1）$\sqrt{\frac{2}{7}}$×$\sqrt{56}$
    （2）$\frac{\sqrt{27}-1}{\sqrt{3}}$
    （3）（$\sqrt{5}$-1）2-$\frac{10}{\sqrt{5}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

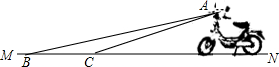    17．齐河路路通电动车厂新开发的一种电动车如图，它的大灯A射出的光线AB，AC 与地面MN 所夹的锐角分别为8°和10°，大灯A与地面的距离为1m则该车大灯照亮地面的宽度BC是1.4m．（不考虑其它因素）
    （参考数据：sin8°=$\frac{4}{25}$，tan8°=$\frac{1}{7}$，sin10°=$\frac{9}{50}$，tan10°=$\frac{5}{28}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．解方程组
    （1）$\left\{\begin{array}{l}4x-3y=5\\ 2x-y=2\end{array}\right.$
    （2）$\left\{\begin{array}{l}\frac{x}{3}+\frac{y}{2}=0\\ 2（x-4）-3（y-1）=3\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

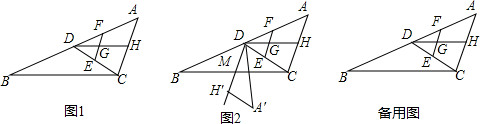    14．如图1，在△ABC中，CD为AB边上的中线，点E、F分别在线段CD、AD上，且$\frac{DF}{DB}=\frac{DE}{DC}$．点G是EF的中点，射线DG交AC于点H．
    （1）求证：△DFE∽△DAC；
    （2）请你判断点H是否为AC的中点？并说明理由；
    （3）若将△ADH绕点D顺时针旋转至△A′DH′，使射线DH′与射线CB相交于点M（不与B，C重合．图2是旋转后的一种情形），请探究∠BMD与∠BDA′之间所满足的数量关系，并加以证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．已知数轴上点A表示的数为6，点B表示的数为-4，动点P表示的数为x．
    （1）若P沿数轴从A向左匀速运动，运动到B点时停止．
    ①写出线段AB的长度是10，线段PB的长度=|x+4|（填“＞”、“=”或“＜”）；
    ②M为AP中点，N为PB中点，点P在运动过程中，线段MN的长度是否发生变化？若变化，请说明理由，若不变，请画出图形，并求出线段MN的长．
    （2）当动点P在数轴这条直线上运动时；
    ①线段PA+PB的长度是否存在最大值或最小值，若存在，请求出这个最大值或最小值，若不存在，请说明理由；
    ②知识迁移：请猜想|x-1|+|x+5|的最值（最大值或最小值），并直接写出结论．
    （3）动点Q从B点出发，以每秒2个单位长度的速度沿数轴匀速运动，动点P从A点出发以每秒6个单位长度向左匀速运动，若两点同时出发若干秒种后，P，Q两点相距2个单位长度，请求出x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．用适当方法解下列方程组：
    （1）$\left\{\begin{array}{l}{y=2x}\\{3x+y=10}\end{array}\right.$   （2）$\left\{\begin{array}{l}{\frac{x}{4}+\frac{y}{3}=3}\\{3x-2（y-1）=20}\end{array}\right.$．

    查看答案和解析>>

    同步练习册答案