
分析 (1)首先计算乘方和开方,然后计算乘法,最后从左向右依次计算,求出算式的值是多少即可.
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分确定出不等式组的解集,即可确定出最小的整数解.
解答 解:(1)原式=$\sqrt{3}$-1-2$\sqrt{3}$+$\sqrt{3}$-1
=-2.
(2)$\left\{\begin{array}{l}{2-x≤3①}\\{\frac{3}{2}x+1>x-\frac{3}{2}②}\end{array}\right.$
解不等式①得x≥-1;
解不等式②得x>-5;
不等式组的解集为x≥-1;
最小整数解为-1.
点评 此题考查了实数的运算,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:解答题
 某学校开展了以“人生观、价值观”为主题的班会活动,活动结束后,九年级某班一小组提出了5个主要观点并在本班50名学生中进行了调查(要求每位同学只选自己最认可的一项观点),并制成了如下扇形统计图.
某学校开展了以“人生观、价值观”为主题的班会活动,活动结束后,九年级某班一小组提出了5个主要观点并在本班50名学生中进行了调查(要求每位同学只选自己最认可的一项观点),并制成了如下扇形统计图.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a+3a2=3a3 | B. | (a-b)2=a2-ab+b2 | C. | 2(a-b)=2a-2b | D. | (2ab)2÷ab=2ab |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
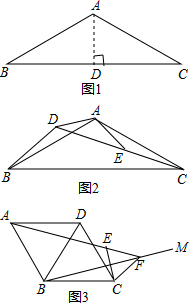 问题背景:如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,∠BAD=$\frac{1}{2}$∠BAC=60°,于是$\frac{BC}{AB}$=$\frac{2BD}{AB}$=$\sqrt{3}$;
问题背景:如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,∠BAD=$\frac{1}{2}$∠BAC=60°,于是$\frac{BC}{AB}$=$\frac{2BD}{AB}$=$\sqrt{3}$;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
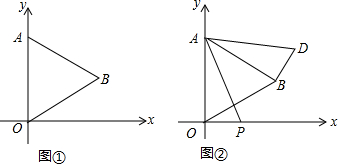
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com