
分析 因为两点P(p+p2+1,q)、Q(-p2+5+q,q)均在二次函数y=ax2+bx+c上,所以对称轴x=-$\frac{b}{2a}$=$\frac{P+{p}^{2}+1-{p}^{2}+5+q}{2}$,所以-$\frac{b}{a}$=6+p+q,设方程ax2+bx+c=0的两根为x1,3x1,则有x1+3x1=6+p+q,求出x1即可解决问题.
解答 解:两点P(p+p2+1,q)、Q(-p2+5+q,q)均在二次函数y=ax2+bx+c上,
∴对称轴x=-$\frac{b}{2a}$=$\frac{P+{p}^{2}+1-{p}^{2}+5+q}{2}$,
∴-$\frac{b}{a}$=6+p+q,设方程ax2+bx+c=0的两根为x1,3x1,
则有x1+3x1=6+p+q,
∴x1=$\frac{6+p+q}{4}$,3x1=$\frac{18+3p+3q}{4}$,
∴方程ax2+bx+c=0的两个根为$\frac{6+p+q}{4}$,$\frac{18+3p+3q}{4}$.
点评 本题考查抛物线与轴的交点、一元二次方程的根与系数关系等知识,解题的关键是灵活运用二次函数的性质以及根与系数关系,属于中考创新题目.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:选择题
| A. | x≥$\sqrt{2}$ | B. | x≤$\sqrt{2}$ | C. | x<$\sqrt{2}$ | D. | x>$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
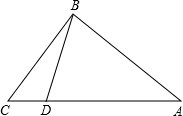 如图,在Rt△ABC中,∠ABC=90°,AB=20,BC=15,点D为AC边上的动点,点D从点C出发,沿边CA往A运动,当运动到点A时停止,设点D运动的时间为t秒,速度为每秒2个单位长度.
如图,在Rt△ABC中,∠ABC=90°,AB=20,BC=15,点D为AC边上的动点,点D从点C出发,沿边CA往A运动,当运动到点A时停止,设点D运动的时间为t秒,速度为每秒2个单位长度.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
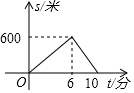 小丽、小亮从学校出发到中心书城购书,小丽步行一段时间后,小亮骑自行车沿相同路线前往,两人均匀前行,他们的路程s(米)与小丽出发时间t(分)之间的函数关系如图,下列说法:①小丽的速度是100米/分;②小丽出发6分钟后小亮才出发;③学校离中心书城的路程为1000米;④小亮骑车的速度是250米/分.其中正确的是( )
小丽、小亮从学校出发到中心书城购书,小丽步行一段时间后,小亮骑自行车沿相同路线前往,两人均匀前行,他们的路程s(米)与小丽出发时间t(分)之间的函数关系如图,下列说法:①小丽的速度是100米/分;②小丽出发6分钟后小亮才出发;③学校离中心书城的路程为1000米;④小亮骑车的速度是250米/分.其中正确的是( )| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
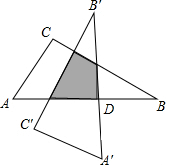 如图,Rt△ABC中,∠C=90°,∠A=60°,AC=6,以斜边AB的中点D为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′,则旋转后两个直角三角形重叠部分的面积为( )
如图,Rt△ABC中,∠C=90°,∠A=60°,AC=6,以斜边AB的中点D为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′,则旋转后两个直角三角形重叠部分的面积为( )| A. | 6 | B. | 9 | C. | 6$\sqrt{3}$ | D. | 9$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9$\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | $\frac{3}{2}$$\sqrt{3}$ | D. | $\frac{1}{4}$$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y2-49x2 | B. | $\frac{1}{49}-{x^4}$ | C. | -m2-n2 | D. | $\frac{1}{4}{(p+q)^2}-9$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com