
【题目】如图,抛物线y=ax2+bx+4与x轴交于A(﹣2,0)、B(4、0)两点,与y轴交于C点.
(1)求抛物线的解析式;
(2)T是抛物线对称轴上的一点,且△ATC是以AC为底的等腰三角形,求点T的坐标;
(3)M、Q两点分别从A、B点以每秒1个单位长度的速度沿x轴同时出发相向而行,当点M到原点时,点Q立刻掉头并以每秒 ![]() 个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点停止运动,过点M的直线l⊥x轴交AC或BC于点P.求点M的运动时间t与△APQ面积S的函数关系式,并求出S的最大值.
个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点停止运动,过点M的直线l⊥x轴交AC或BC于点P.求点M的运动时间t与△APQ面积S的函数关系式,并求出S的最大值.
【答案】
(1)解:把A(﹣2,0),B(4,0)代入y=ax2+bx+4得:
![]() ,
,
解得:a=﹣ ![]() ,b=1,
,b=1,
∴抛物线的解析式是:y=﹣ ![]() x2+x+4,
x2+x+4,
答:抛物线的解析式是y=﹣ ![]() x2+x+4
x2+x+4
(2)解:由y=﹣ ![]() x2+x+4=﹣
x2+x+4=﹣ ![]() (x﹣1)2+
(x﹣1)2+ ![]() ,得抛物线的对称轴为直线x=1,
,得抛物线的对称轴为直线x=1,
直线x=1交x轴于点D,设直线x=1上一点T(1,h),
连接TC、TA,作CE⊥直线x=1,垂足是E,
由C(0,4)得点E(1,4),
在Rt△ADT和Rt△TEC中,由TA=TC得32+h2=12+(4﹣h)2,
∴h=1,
∴T的坐标是(1,1),
答:点T的坐标是(1,1)
(3)解:(I)当0<t≤2时,△AMP∽△AOC,
∴ ![]() =
= ![]() ,PM=2t,
,PM=2t,
AQ=6﹣t,
∴S= ![]() PMAQ=
PMAQ= ![]() ×2t(6﹣t)=﹣t2+6t=﹣(t﹣3)2+9,
×2t(6﹣t)=﹣t2+6t=﹣(t﹣3)2+9,
当t=2时S的最大值为8;
(II)当2<t≤3时,
作PM⊥x轴于M,作PF⊥y轴于点F,
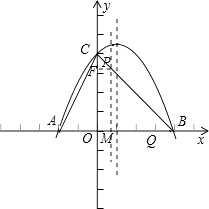
则△COB∽△CFP,
又∵CO=OB,
∴FP=FC=t﹣2,PM=4﹣(t﹣2)=6﹣t,AQ=4+ ![]() (t﹣2)=
(t﹣2)= ![]() t+1,
t+1,
∴S= ![]() PMAQ=
PMAQ= ![]() (6﹣t)(
(6﹣t)( ![]() t+1)=﹣
t+1)=﹣ ![]() t2+4t+3=﹣
t2+4t+3=﹣ ![]() (t﹣
(t﹣ ![]() )2+
)2+ ![]() ,
,
当t= ![]() 时,S最大值为
时,S最大值为 ![]() ,
,
综合(I)(II)S的最大值为 ![]() ,
,
答:点M的运动时间t与△APQ面积S的函数关系式是S=﹣t2+6t(0<t≤2),S=﹣ ![]() t2+4t+3(2<t≤3),S的最大值是
t2+4t+3(2<t≤3),S的最大值是 ![]() .
.
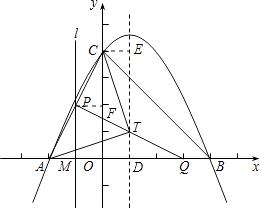
【解析】(1)把A、B的坐标代入抛物线的解析式得到方程组,求出方程组的解即可;(2)设直线x=1上一点T(1,h),连接TC、TA,作CE⊥直线x=1,垂足是E,根据TA=TC由勾股定理求出即可;(3)(I)当0<t≤2时,△AMP∽△AOC,推出比例式,求出PM,AQ,根据三角形的面积公式求出即可;(II)当2<t≤3时,作PM⊥x轴于M,PF⊥y轴于点F,表示出三角形APQ的面积,利用配方法求出最值即可.


科目:初中数学 来源: 题型:
【题目】如图,AB⊥BC,DC⊥BC,垂足分别为B、C,设AB=4,DC=1,BC=4.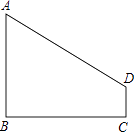
(1)求线段AD的长.
(2)在线段BC上是否存在点P,使△APD是等腰三角形?若存在,求出线段BP的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察如图所示的长方体.

(1)用符号表示下列两棱的位置关系:AB___A′B′,AA′_____AB,D′A′_____D′C′,AD______BC.
(2) A′B′与BC所在的直线是两条不相交的直线,它们_____平行线.(填“是”或“不是”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校准备组织七年级学生参加夏令营,已知:用3辆小客车和1辆大客车每次可运送学生105人;用一辆小客车和2辆大客车每次可运送学生110人,现有学生400人,计划租用小客车a辆,大客车b辆,一次送完,且恰好每辆车都坐满.
(1)1辆小客车和1辆大客车都坐满后一次可送多少名学生?
(2)请你帮学校设计出所有的租车方案;
(3)若小客车每辆需租金200元,大客车每辆需租金380元,请选出最省钱的方案,并求出最省租金.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 和
和![]() 都是边长为1的等边三角形.
都是边长为1的等边三角形.
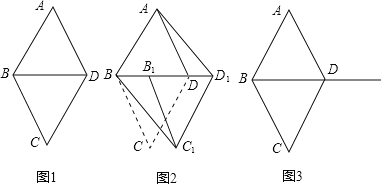
![]() 四边形ABCD是菱形吗?为什么?
四边形ABCD是菱形吗?为什么?
![]() 如图2,将
如图2,将![]() 沿射线BD方向平移到
沿射线BD方向平移到![]() 的位置,则四边形
的位置,则四边形![]() 是平行四边形吗?为什么?
是平行四边形吗?为什么?
![]() 在
在![]() 移动过程中,四边形
移动过程中,四边形![]() 有可能是矩形吗?如果是,请求出点B移动的距离
有可能是矩形吗?如果是,请求出点B移动的距离![]() 写出过程
写出过程![]() ;如果不是,请说明理由
;如果不是,请说明理由![]() 图3供操作时使用
图3供操作时使用![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
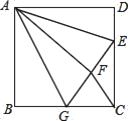
【题目】如图,正方形ABCD中,AB=12,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论: ①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=28.8. 其中正确结论的个数是( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为建设资源节约型、环境友好型社会,克服因干旱而造成的电力紧张困难,切实做好节能减排工作.某地决定对居民家庭用电实行“阶梯电价”,电力公司规定:居民家庭每月用电量在80千瓦时以下(含80千瓦时,1千瓦时俗称1度)时,实行“基本电价”;当居民家庭月用电量超过80千瓦时时,超过部分实行“提高电价”.
(1)小张家今年2月份用电100千瓦时,上缴电费68元;5月份用电120千瓦时,上缴电费88元.求“基本电价”和“提高电价”分别为多少元/千瓦时;
(2)若6月份小张家预计用电130千瓦时,请预算小张家6月份应上缴的电费.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com