
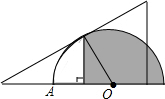
 如图,将一块含30°角的直角三角板和半圆量角器按如图的方式摆放,使斜边与半圆相切.若半径OA=2,则图中阴影部分的面积为$\frac{4π}{3}$+$\frac{\sqrt{3}}{2}$.(结果保留π)
如图,将一块含30°角的直角三角板和半圆量角器按如图的方式摆放,使斜边与半圆相切.若半径OA=2,则图中阴影部分的面积为$\frac{4π}{3}$+$\frac{\sqrt{3}}{2}$.(结果保留π) 分析 图中阴影部分的面积=扇形BOD的面积+△BOC的面积.
解答  解:∵斜边与半圆相切,点B是切点,
解:∵斜边与半圆相切,点B是切点,
∴∠EBO=90°.
又∵∠E=30°,
∴∠EBC=60°.
∴∠BOD=120°,
∵OA=OB=2,
∴OC=$\frac{1}{2}$OB=1,BC=$\sqrt{3}$.
∴S阴影=S扇形BOD+S△BOC=$\frac{120π×{2}^{2}}{360}$+$\frac{1}{2}$×1×$\sqrt{3}$=$\frac{4π}{3}$+$\frac{\sqrt{3}}{2}$.
故答案是:$\frac{4π}{3}$+$\frac{\sqrt{3}}{2}$.
点评 本题考查了切线的性质,扇形面积的计算.此题利用了“分割法”求得阴影部分的面积.


科目:初中数学 来源: 题型:选择题
| A. | 1.34×102 | B. | 1.34×103 | C. | 1.34×104 | D. | 1.34×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
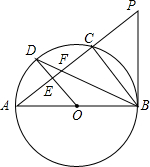 已知⊙O是以AB为直径的△ABC的外接圆,OD∥BC交⊙O于点D,交AC于点E,连接AD、BD,BD交AC于点F.
已知⊙O是以AB为直径的△ABC的外接圆,OD∥BC交⊙O于点D,交AC于点E,连接AD、BD,BD交AC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 单程所花时间 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 45 |
| 人数 | 3 | 3 | 6 | 12 | 2 | 2 | 1 | 1 |
| A. | 众数是12 | B. | 平均数是18 | C. | 极差是45 | D. | 中位数是20 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
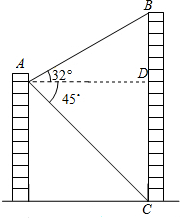 如图,从一个建筑物的A处测得对面楼BC的顶部B的仰角为32°,底部C的俯角为45°,观测点与楼的水平距离AD为31m,则楼BC的高度约为50m(结果取整数).(参考数据:sin32°≈0.5,cos32°≈0.8,tan32°≈0.6)
如图,从一个建筑物的A处测得对面楼BC的顶部B的仰角为32°,底部C的俯角为45°,观测点与楼的水平距离AD为31m,则楼BC的高度约为50m(结果取整数).(参考数据:sin32°≈0.5,cos32°≈0.8,tan32°≈0.6)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com