
分析 首先假设每件围巾应降价x元,即可得出(80-x)(100+$\frac{x}{10}$×20)=8400,即可求出x的值,进而得出y=(80-x)(100+2x)求出最值即可.
解答 解:设若想平均每天销售这种围巾盈利8400元,并使顾客得到更大的实惠,那么每件围巾应降价x元,根据题意得:
(80-x)(100+$\frac{x}{10}$×20)=8400,
解这个方程组得:
x1=10,x2=20,
为使顾客得到更大的实惠x=20;
答:想平均每天销售这种围巾盈利8400元,并使顾客得到更大的实惠,那么每件围巾应降价20元.
设:每件围巾应降价x元,设降价x元时,盈利为y元,则 y=(80-x)(100+$\frac{x}{10}$×20)0<x<80,
因为y=(80-x)(100+$\frac{x}{10}$×20),
=(80-x)(100+2x)
=8000+160x-100x-2x2
=-2x2+60x+8000
=-2(x-15)2+8450
所以当x=15时,y最大值=8450,
答:若想获利最大,应降价15元.
点评 此题主要考查了二次函数的最值问题以及一元二次方程的应用,根据已知得出二次函数的最值时是中考中考查重点,同学们应重点掌握.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:解答题
| 少分数段(x表示分数) | 频数 | 频率 |
| 50≤x<60 | 4 | 0.1 |
| 60≤x<70 | a | 0.2 |
| 70≤x<80 | 12 | b |
| 80≤x<90 | 10 | 0.25 |
| 90≤x<100 | 6 | 0.15 |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
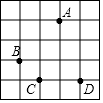 如图,每个小正方形的边长都是1,图中A,B,C,D四个点分别为小正方形的顶点,下列说法:
如图,每个小正方形的边长都是1,图中A,B,C,D四个点分别为小正方形的顶点,下列说法:| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
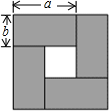 如图,是用四张相同的长方形纸片拼成的图形,其中长方形纸片的长为a,宽为b.请利用图中空白部分的面积的不同表示方法写出一个关于a,b的恒等式(a-b)2=(a+b)2-4ab.
如图,是用四张相同的长方形纸片拼成的图形,其中长方形纸片的长为a,宽为b.请利用图中空白部分的面积的不同表示方法写出一个关于a,b的恒等式(a-b)2=(a+b)2-4ab.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com