
 如图,正方形ABCD的边长为4,点E是BC的中点,AF=3BF,点P为对角线AC上一动点,则FP+EP的最小值是( )
如图,正方形ABCD的边长为4,点E是BC的中点,AF=3BF,点P为对角线AC上一动点,则FP+EP的最小值是( )| A. | $\sqrt{15}$ | B. | $\sqrt{17}$ | C. | 5 | D. | 4$\sqrt{2}$ |
分析 首先作点E关于AC的对称点M,连接FM,过点F作FN⊥CD于点N,由四边形ABCD是正方形,可得M是CD的中点,PM是FP+EP的最小值,然后利用勾股定理求解即可求得答案.
解答 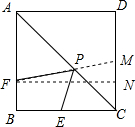 解:作点E关于AC的对称点M,连接FM,过点F作FN⊥CD于点N,
解:作点E关于AC的对称点M,连接FM,过点F作FN⊥CD于点N,
∵四边形ABCD是正方形,
∴M是CD的中点,PM是FP+EP的最小值,
∵正方形ABCD的边长为4,点E是BC的中点,AF=3BF,
∴BF=$\frac{1}{4}$AB=1,CM=CE=$\frac{1}{2}$BC=2,
∵四边形BCNP是矩形,
∴FN=BC=4,CN=BF=1,
∴MN=CM-CN=1,
∴FM=$\sqrt{F{N}^{2}+M{N}^{2}}$=$\sqrt{17}$.
即FP+EP的最小值是:$\sqrt{17}$.
故选B.
点评 此题考查了最短路径问题以及正方形的性质.注意准确找到点P的位置是解此题的关键.


科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | ±$\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | ±2$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{90}{x}=\frac{60}{x-6}$ | B. | $\frac{90}{x-6}=\frac{60}{x}$ | C. | $\frac{90}{x+6}=\frac{60}{x}$ | D. | $\frac{90}{x}=\frac{60}{x+6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 数据的个数和方差 | B. | 数据的平均数和数据的个数 | ||
| C. | 数据的个数和数据的平均数 | D. | 数据的方差和数据的平均数 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在平行四边形ABCD中,对角线AC和BD交于点O,E是CD的中点,连接OE,若AD=5,CD=4,则OE的长为( )
在平行四边形ABCD中,对角线AC和BD交于点O,E是CD的中点,连接OE,若AD=5,CD=4,则OE的长为( )| A. | 2 | B. | 2.5 | C. | 3 | D. | 3.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 早上太阳从西方升起 | |
| B. | 将油滴入水中,油会浮在水面上 | |
| C. | 抛出的石头会下落 | |
| D. | 掷一枚骰子,向上一面的数字是偶数 |
查看答案和解析>>
科目:初中数学 来源:2017届江苏省宜兴市宜城环科园教学联盟九年级下学期第一次质量检测数学试卷(解析版) 题型:判断题
如图1,已知点A(a,0),B(0,b),且a、b满足  ,?ABCD的边AD与y轴交于点
,?ABCD的边AD与y轴交于点 E,且E为AD中点,双曲线y=
E,且E为AD中点,双曲线y= 经过C、D两点.
经过C、D两点.
(1)求k的值;
(2)点P在双曲线y =
=  上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;
上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;
(3)以线段AB为对角线作正方形AFBH(如图3),点T是边AF上一动点,M是HT的中点,MN⊥HT,交AB于N,当T在AF上运动时,  的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值
的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值 ,并给出你的证明.
,并给出你的证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com