
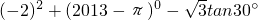
 ×
×
 ,
, ,x2=1-
,x2=1- ;
; ,
, ,x2=2-
,x2=2- .
.

 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 下面是两位同学的一段对话:
下面是两位同学的一段对话:查看答案和解析>>
科目:初中数学 来源: 题型:
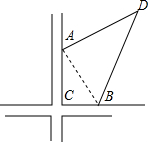 如图,李伯伯承包了一块四边形的土地ABCD,他让小亮帮他测量一下这块地的面积.先量得AC的长为120米,BC的长为60米,BD的长为240米.当要测量AD的长度时,小亮说:“不用量了,我已经测得BA恰好平分∠CAB,公路AC和BC是互相垂直的,有了这些条件,就能求出这块土地的面积了.”小亮说得对吗?你会计算这块土地的面积吗?
如图,李伯伯承包了一块四边形的土地ABCD,他让小亮帮他测量一下这块地的面积.先量得AC的长为120米,BC的长为60米,BD的长为240米.当要测量AD的长度时,小亮说:“不用量了,我已经测得BA恰好平分∠CAB,公路AC和BC是互相垂直的,有了这些条件,就能求出这块土地的面积了.”小亮说得对吗?你会计算这块土地的面积吗?查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com