练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．下列五家银行行标中，既是中心对称图形，又是轴对称图形的个数有（　　）
    A．4个B．3个C．2个D．1个

    分析 根据轴对称图形和中心对称图形的概念对各图形分析判断即可得解．

    解答 解：第一个图形既是中心对称图形，又是轴对称图形，
    第二个图形不是中心对称图形，是轴对称图形，
    第三个图形既是中心对称图形，又是轴对称图形，
    第四个图形不是中心对称图形，也不是轴对称图形，
    第五个图形是中心对称图形，不是轴对称图形，
    综上所述，既是中心对称图形，又是轴对称图形的有2个．
    故选C．

    点评 本题考查了中心对称图形与轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    15．方程x-1=5+2x的解为（　　）
    A．.x=-2B．x=2C．x=-6D．x=6

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．下列实数最小的是（　　）
    A．$\sqrt{2}$B．$\frac{\sqrt{2}}{2}$C．$\sqrt{2}$-1D．2-$\sqrt{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

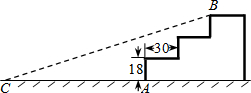    13．如图，某公园入口有三级台阶，每级台阶高18cm，深30cm，拟将台阶改为斜坡，设台阶的起点为A，斜坡的起始点为C，现设计斜坡BC的坡度i=1：5，则AC的长度是（　　）
    A．270cmB．210cmC．180cmD．96cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．在函数y=$\frac{\sqrt{3-x}}{x+2}$中，自变量x的取值范围是（　　）
    A．x≤3且x≠-2B．x≤3C．x≠-2D．x＜3且x≠-2

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．如图，直角边长为$\sqrt{2}$的等腰直角三角形与边长为3的等边三角形在同一水平线上，等腰直角三角形沿水平线从左向右匀速穿过等边三角形时，设穿过时间为t，两图形重合部分的面积为S，则S关于t的图象大致为（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．合肥热线讯 1月10日上午9时，合肥市第十五届人民代表大会第六次会议在合肥大剧院开幕，从会议中得知：合肥市实现了“十三五”良好开局，2016年全市生产总值6200亿元，这里的数字“6200亿”用科学记数法表示为（　　）
    A．6.2×108B．6.2×109C．6.2×1010D．6.2×1011

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．如图1，在平面直角坐标系xOy中，直线EF：y=kx+3与x轴，y轴分别交点E，F，△OEF为等腰直角三角形．
    （1）求k的值；
    （2）菱形ABCD的顶点A的坐标为（2，0），点B的坐标为（0，1），点C在第一象限，对角线BD与x轴平行，将菱形ABCD沿x轴向左平移m个单位，当点D落在△EOF的内部时（不包括三角形的边），求m的取值范围；
    （3）如图2，直线PQ：y=$\frac{1}{2}$x+2交x轴于点Q，点P（2，n），点M为PQ上一点，点S在x轴正半轴上，连接PS，过S作ST⊥PS，交y轴于点T，点G（-1，0），作射线MG交ST于点N，若PS=NS，求点M的坐标．

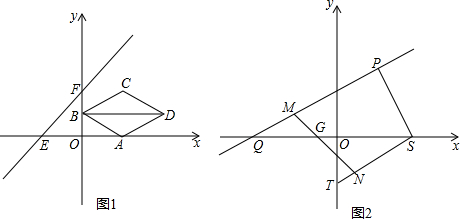
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．甲、乙两人进行羽毛球比赛，甲发出一个十分关键的球，出手点为P，羽毛球距地面高度h（米）与其飞行的水平距离s（米）之间的关系式为h=-$\frac{1}{12}$s2+$\frac{2}{3}$s+$\frac{3}{2}$．如图，已知球网AB距原点5米，乙（用线段CD表示）扣球的最大高度为$\frac{9}{4}$米，设乙的起跳点C的横坐标为m，若乙原地起跳，因球的高度高于乙扣球的最大高度而导致接球失败，则m的取值范围是（　　）
    A．4＜m＜8+$\sqrt{7}$B．4-$\sqrt{7}$＜m＜5C．5＜m＜9D．5＜m＜4+$\sqrt{7}$

    查看答案和解析>>

    同步练习册答案