
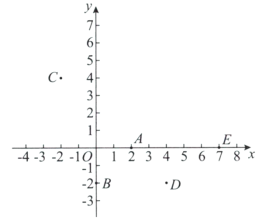
【题目】如图,在平面直角坐标系![]() 中,有五个点
中,有五个点![]() ,将二次函数
,将二次函数![]() 的图象记为W.下列的判断中
的图象记为W.下列的判断中
①点A一定不在W上;
②点B,C,D可以同时在W上;
③点C,E不可能同时在W上.
所有正确结论的序号是_________.
【答案】①②
【解析】
由m≠0可得点A 不在抛物线上,故可判断①;先根据B,C两点坐标求出函数关系式,再把D点坐标代入即可判断点D是否在函数图象上;将C、E两点坐标代入![]() ,能求出a,m则可判断出C、E均在函数图象上,否则,则不在函数图象上.
,能求出a,m则可判断出C、E均在函数图象上,否则,则不在函数图象上.
由二次函数![]() 知其顶点坐标为(2,m),而m≠0,
知其顶点坐标为(2,m),而m≠0,
故(2,0)不在函数图象上,
所以,点A不在函数图象上,即点A一定不在W上,故①正确;
把C(-2,4),B(0,-2)代入![]() 得,
得,
![]() ,
,
解得,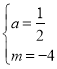 ,
,
∴![]()
当x=4时,y=-2,
所以,点D在函数![]() 的图象上,
的图象上,
因此,点B,C,D可以同时在W上,故②正确;
把C(-2,4),E(7,0)分别代入![]() 得,
得,
![]() ,
,
解得,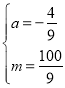
∴![]()
所以,点C,E可能同时在W上,故③错误.
故答案为:①②.


科目:初中数学 来源: 题型:
【题目】五一黄金周,小张一家自驾去某景点旅行.已知汽车油箱的容积为50L,小张爸爸把油箱加满油后到了离加油站200km的某景点,第二天沿原路返回.
(1)油箱加满油后,求汽车行驶的总路程s(单位:km)与平均耗油量b(单位L/km)的函数关系式;
(2)小张爸爸以平均每千米耗油0.1L的速度驾驶到达目的地,返程时由于下雨,降低了车速,此时平均每千米的耗油量增加了一倍.如果小张爸爸始终以此速度行驶,不需要加油能否返回原加油站?如果不能,至少还需加多少油?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 从
从![]() 点出发,以每秒2个单位长度的速度,按
点出发,以每秒2个单位长度的速度,按![]() 的顺序在边上匀速运动,设
的顺序在边上匀速运动,设![]() 点的运动时间为
点的运动时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() ,
,![]() 关于
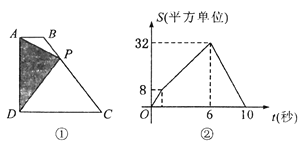
关于![]() 的函数图像如图②所示,当
的函数图像如图②所示,当![]() 运动到
运动到![]() 中点时,
中点时,![]() 的面积为__________.
的面积为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司经过市场调查,发现某种运动服的销量与售价是一次函数关系,具体信息如下表:
售价(元/件) | 200 | 210 | 220 | 230 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件150元.
(1)售价为![]() 元,月销量为
元,月销量为![]() 件;
件;
①求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
②若销售该运动服的月利润为![]() 元,求
元,求![]() 关于
关于![]() 的函数关系式,并求月利润最大时的售价;
的函数关系式,并求月利润最大时的售价;
(2)由于运动服进价降低了![]() 元,商家决定回馈顾客,打折销售,这时月销量与调整后的售价仍满足(1)中函数关系式.结果发现,此时月利润最大时的售价比调整前月利润最大时的售价低15元,则
元,商家决定回馈顾客,打折销售,这时月销量与调整后的售价仍满足(1)中函数关系式.结果发现,此时月利润最大时的售价比调整前月利润最大时的售价低15元,则![]() 的值是多少?
的值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P是平面内任意一点,点A,B是![]() 上不重合的两个点,连结
上不重合的两个点,连结![]() .当
.当![]() 时,我们称点P为
时,我们称点P为![]() 的“关于
的“关于![]() 的关联点”.
的关联点”.

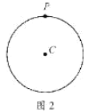
(1)如图2,当点P在![]() 上时,点P是
上时,点P是![]() 的“关于
的“关于![]() 的关联点”时,画出一个满足条件的
的关联点”时,画出一个满足条件的![]() ,并直接写出
,并直接写出![]() 的度数;
的度数;
(2)在平面直角坐标系中有点![]() ,点M关于y轴的对称点为点N.
,点M关于y轴的对称点为点N.
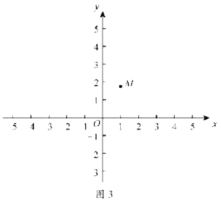
①以点O为圆心,![]() 为半径画
为半径画![]() ,在y轴上存在一点P,使点P为
,在y轴上存在一点P,使点P为![]() “关于
“关于![]() 的关联点”,直接写出点P的坐标;
的关联点”,直接写出点P的坐标;
②点![]() 是x轴上一动点,当
是x轴上一动点,当![]() 的半径为1时,线段
的半径为1时,线段![]() 上至少存在一点是
上至少存在一点是![]() 的“关于某两个点的关联点”,求m的取值范围.
的“关于某两个点的关联点”,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知二次函数
中,已知二次函数![]() 的图象与x轴交于点
的图象与x轴交于点![]() ,与y轴交于点B,将其图象在点A,B之间的部分(含A,B两点)记为F.
,与y轴交于点B,将其图象在点A,B之间的部分(含A,B两点)记为F.
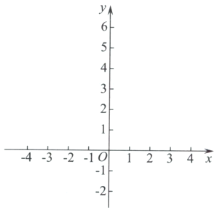
(1)求点B的坐标及该函数的表达式;
(2)若二次函数![]() 的图象与F只有一个公共点,结合函数图象,求a的取值范围.
的图象与F只有一个公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
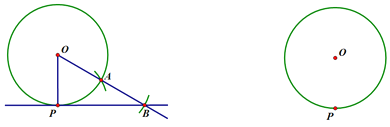
【题目】已知⊙O及⊙O上一点P,过点P作⊙O的切线.
小明设计了如下尺规作法:
①连接OP,以点P为圆心,OP长为半径画弧交⊙O于点A;
②连接OA,延长OA到B,使AB=OA,作直线PB.则直线即为所求作.
(1)请证明小明作法的正确性;
(2)请你自己再设计一种尺规作图方法(保留痕迹,不要证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1.在![]() 中,
中,![]() 把
把![]() 沿对角线
沿对角线![]() 所在的直线折叠,使点
所在的直线折叠,使点![]() 落在点
落在点![]() 处,
处,![]() 交
交![]() 于点
于点![]() .连接
.连接![]() .
.
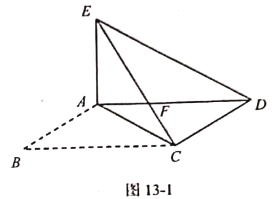
(1)求证:![]() ;
;
(2)求证:![]() 为等腰三角形;
为等腰三角形;
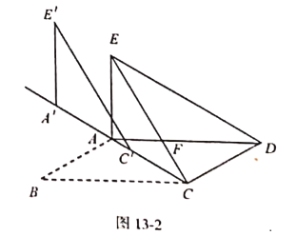
(3)将图1中![]() 的沿射线
的沿射线![]() 方向平移得到
方向平移得到![]() (如图2所示) .若在
(如图2所示) .若在![]() 中,
中,![]() . 当
. 当![]() 时,直接写出
时,直接写出![]() 平移的距离.
平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
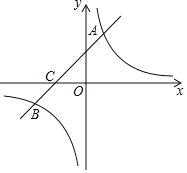
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于第一、三象限内的
的图象相交于第一、三象限内的![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
⑴求该反比例函数和一次函数的解析式;
⑵在![]() 轴上找一点
轴上找一点![]() 使
使![]() 最大,求
最大,求![]() 的最大值及点
的最大值及点![]() 的坐标;
的坐标;
⑶直接写出当![]() 时,
时,![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com