
【题目】已知△ABC和△CDE都为等腰直角三角形,∠ACB=∠ECD=90°.
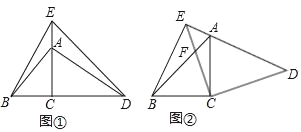
探究:如图①,当点A在边EC上,点C在线段BD上时,连结BE、AD.求证:BE=AD,BE⊥AD.
拓展:如图②,当点A在边DE上时,AB、CE交于点F,连结BE.若AE=2,AD=4,则![]() 的值为 .
的值为 .
【答案】(1)见解析;(2)![]()
【解析】
(1)根据等腰三角形得BC=CA,EC=CD,证明△BCE≌△ACD,根据同角的余角相等即可证明,(2)作辅助线证明FM=FN,根据S△ABE=S△BEF+S△AEF,求出EF,FC的长即可求![]() 的值.
的值.
解:(1)探究:延长DA交BE于F.
∵△ABC和△CDE都为等腰直角三角形,∠ACB=∠ECD=90°.
∴BC=CA,EC=CD,
∴△BCE≌△ACD,
∴BE=AD,∠BEC=∠ADC,
∵∠ACB=90°,
∴∠BEC+∠EBC=90°,
∴∠ADC+∠EBC=90°,
∴∠BFD=90°,
∴BE⊥AD.
(2)拓展:作FM⊥DE于M,FN⊥BE于N.
由探究可知:BE⊥DE,BE=AD=4,∠FEM=∠FEB=45°,
∵FM⊥DE于M,FN⊥BE于N.
∴FM=FN,
∵![]() EBFN+
EBFN+![]() AEFM=
AEFM=![]() BEAE,
BEAE,
∴FM=FN=![]() ,
,
∴EF=![]() ,
,
∵CE=CD=3![]() ,
,
∴CF=![]() ,
,
∴EF:CF=4:5.
故答案为![]() .
.


科目:初中数学 来源: 题型:
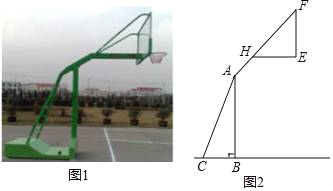
【题目】如图1,2分别是某款篮球架的实物图与示意图,已知AB⊥BC于点B,底座BC的长为1米,底座BC与支架AC所成的角∠ACB=60°,点H在支架AF上,篮板底部支架EH∥BC,EF⊥EH于点E,已知AH长![]() 米,HF长
米,HF长![]() 米,HE长1米.
米,HE长1米.
(1)求篮板底部支架HE与支架AF所成的角∠FHE的度数.
(2)求篮板底部点E到地面的距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示:在△ABC中,AB=AC=5,BC=8,D,E分别为BC.AB边上一点,∠ADE=∠C,
(1)求证:AD2=AEAB;
(2)∠ADC与∠BED是否相等?请说明理由;
(3)若CD=2,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
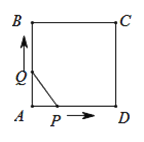
【题目】如图,正方形![]() 的边长为
的边长为![]() ,点
,点![]() ,点
,点![]() 同时从点
同时从点![]() 出发,速度均2cm/s,点
出发,速度均2cm/s,点![]() 沿
沿![]() 向点
向点![]() 运动,点
运动,点![]() 沿
沿![]() 向点
向点![]() 运动,则△
运动,则△![]() 的面积
的面积![]() 与运动时间
与运动时间![]() 之间函数关系的大致图象是( )
之间函数关系的大致图象是( )
A. 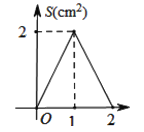 B.
B. 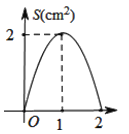 C.
C. 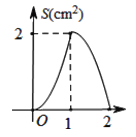 D.
D. 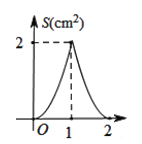
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC,∠A、∠B、∠C之和为多少?为什么?
解:∠A+∠B+∠C=180°
理由:作∠ACD=∠A,并延长BC到E
∵∠ACD=∠ (已作)
AB∥CD( )
∴∠B= ( )
而∠ACB+∠ACD+∠DCE=180°
∴∠ACB+ + =180°( )
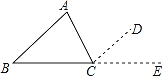
查看答案和解析>>
科目:初中数学 来源: 题型:
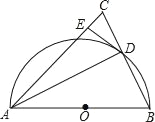
【题目】如图,在△ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD.过点D作DE⊥AC,垂足为点E.
(1)求证:DE是⊙O的切线;
(2)当⊙O半径为3,CE=2时,求BD长.
查看答案和解析>>
科目:初中数学 来源: 题型:
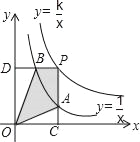
【题目】反比例函数y=![]() 和y=
和y=![]() 在第一象限内的图象如图所示,点P在y=
在第一象限内的图象如图所示,点P在y=![]() 的图象上,PC⊥x轴,交y=
的图象上,PC⊥x轴,交y=![]() 的图象于点A,PD⊥y轴,交y=
的图象于点A,PD⊥y轴,交y=![]() 的图象于点B,当点P在y=
的图象于点B,当点P在y=![]() 的图象上运动时,以下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;其中一定正确的是( )
的图象上运动时,以下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;其中一定正确的是( )
A. ①②③ B. ① C. ②③ D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+3a过点A(﹣1,0).
(1)求抛物线的对称轴;
(2)直线y=x+4与y轴交于点B,与该抛物线对称轴交于点C.如果该抛物线与线段BC有交点,结合函数的图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
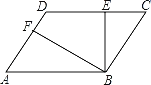
【题目】如图,在平行四边形ABCD中,BE⊥CD,BF⊥AD,垂足分别为E,F,CE=2,DF=1,∠EBF=60°,则平行四边形ABCD的周长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com