
����Ŀ��Ϊȫ��᳹���Ľ������룬��֡�������һ�Ľ�������ٽ�ѧ�������ɳ���������ʽ���ˮƽ���ɶ��е��������п�ʵʩ��������ֵ������60����1000��Ů80�ף��ؿ�����������������ѡһ��������2019���^����ѧ�����꼶��ʼʵʩ��ij1ѧΪ�˽����꼶ѧ�������������˶���ϲ������������꼶ѧ���������ȡ����ѧ�����е����ʾ���ͨ������������������������ͳ��ͼ�����������ͳ��ͼ�е���Ϣ�ش���������:
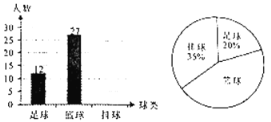
��1�����������ѧ���У�ϲ�������˶���ѧ������������ȫ����ͼ
��2��������ѧ���꼶����400��ѧ����������Ƹ���ѧ���꼶ѧ����ϲ�������˶���ѧ���ж�������
��3������ϲ�������˶���2��������2��Ů���������ȡ2��ѧ����ȷ��Ϊ��У�����˶�Ա���ص��������������б�������״ͼ�ķ������ȡ������ѧ��Ϊһ��������һ��Ů���ĸ���.
���𰸡���1��21��ͼ�μ���������2��180����3��![]()
��������
��1���ȸ���������������ٷֱ����������������������������������ռ�������İٷֱȿɵ��������������ɲ�ȫͼ�Σ�
��2�����������������壬�����ϲ�������˶������İٷֱȣ�Ȼ����400������������ռ�ٷֱȣ����ɵõ�ϲ�������˶�������
��3������״ͼ�ó����еȿ��ܵ���������ҳ�1��������1��Ů��������������ݸ��ʹ�ʽ���ɵó�������ʣ�
�⣺��1��![]() ���ˣ���
���ˣ���
![]() ���ˣ�.
���ˣ�.
���ԣ���������ѧ���У�ϲ�������˶���ѧ����21��.
��ȫ����ͼ���£�

��2��![]() ���ˣ�.
���ˣ�.
���ԣ�����ѧ���꼶ѧ���У�ϲ�������˶���ѧ����180��.
��3��

����12�ֵȿ������������1����2��������1��Ů1��������1��Ů2��������2����1��������2��Ů1��������2��Ů2������Ů1����1������Ů1����2������Ů1��Ů2������Ů2����1������Ů2����2������Ů2��Ů1�������У�1��������1��Ů����8��.
���ԣ��鵽1��������1��Ů���ĸ���![]() .
.


 ���ѵ����Ԫ��ĩ���100��ϵ�д�
���ѵ����Ԫ��ĩ���100��ϵ�д� ��˼άС�ھ�100����ҵ��ϵ�д�
��˼άС�ھ�100����ҵ��ϵ�д� ��ʦָ��һ��ͨϵ�д�
��ʦָ��һ��ͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳����г����飬���ֽ���Ϊ40Ԫ��̨��ÿ�µ�������y��̨�����ۼ�x��Ԫ���������Ϣ���£�
�ۼ�x��Ԫ�� | 50 | 60 | 70 | 80 | ���� |
������y��̨�� | 200 | 180 | 160 | 140 | ���� |
��1��������ѧ���ĺ���������y��x�Ĺ�ϵ����������������� �����������������ϵʽ��
��2���ۼ�Ϊ����Ԫʱ�����µ����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��![]() ��˫����
��˫����![]() ��x>0�����ڵ�
��x>0�����ڵ�![]() ��
��

��1����a��k��ֵ��
��2����ֱ֪��![]() ����
����![]() ��ƽ����ֱ��
��ƽ����ֱ��![]() ����P��m��n����m>3����ֱ��
����P��m��n����m>3����ֱ��![]() ��һ���㣬����P�ֱ���
��һ���㣬����P�ֱ���![]() �ᡢ
�ᡢ![]() ���ƽ���ߣ���˫����
���ƽ���ߣ���˫����![]() ��x>0���ڵ�
��x>0���ڵ�![]() ��
��![]() ��˫�����ڵ�M��N֮��IJ������߶�PM��PN��Χ�ɵ��������߽磩��Ϊ
��˫�����ڵ�M��N֮��IJ������߶�PM��PN��Χ�ɵ��������߽磩��Ϊ![]() ���ᡢ�����궼�������ĵ�������㣮
���ᡢ�����궼�������ĵ�������㣮
�ٵ�![]() ʱ��ֱ��д������
ʱ��ֱ��д������![]() �ڵ������������������
�ڵ������������������![]() �ڵ��������������8�������ͼ����m��ȡֵ��Χ��
�ڵ��������������8�������ͼ����m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����ABCD���ܳ�Ϊ12��E��F��G��HΪ����ABCD�ĸ����е�����AB��x���ı���EFGH�����Ϊy.
(1)��ֱ��д��y��x֮��ĺ�����ϵʽ��
(2)����(1)�еĺ�����ϵʽ�����㵱xΪ��ֵʱ��y�������������ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
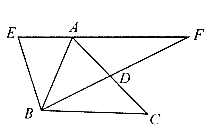
����Ŀ����ͼ����֪![]() �У�
�У�![]() ��D���߶�AC��һ�㣨����A,C�غϣ�,����BD����
��D���߶�AC��һ�㣨����A,C�غϣ�,����BD����![]() ��AB���ۣ�ʹ��D���ڵ�E�����ӳ�BD��EA���ӳ��߽��ڵ�F����
��AB���ۣ�ʹ��D���ڵ�E�����ӳ�BD��EA���ӳ��߽��ڵ�F����![]() ��ֱ�������Σ���AF�ij�Ϊ_________.
��ֱ�������Σ���AF�ij�Ϊ_________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
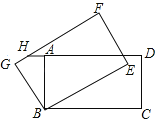
����Ŀ����ͼ���ھ���ABCD�У�AB��4��BC��6��������ABCD��B��ʱ����ת30���õ�����GBEF���ӳ�DA��FG�ڵ�H����GH�ij�Ϊ��������
A.8��4![]() B.
B.![]() ��4C.3
��4C.3![]() ��4D.6��3
��4D.6��3![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�������y��x2+bx+c��x����A����1��0����B��3��0�����㣬��y���ڵ�C��
��1����ͼ1���������ߵĽ���ʽ��
��2����ͼ2����P�ǵ�һ�����������ϵ�һ�����㣬����CP��x���ڵ�E������P��PK��x�ύ�������ڵ�K����y���ڵ�N������AN��EN��AC�����P�ĺ�����Ϊt���ı���ACEN�����ΪS����S��t֮��ĺ�����ϵʽ����Ҫ��д���Ա���t��ȡֵ��Χ����
��3����ͼ3���ڣ�2���������£���F��PC�е㣬����K��PC�Ĵ��������Fƽ����x���ֱ�߽��ڵ�H��KH��CP����QΪ��һ������ֱ��KP�·���������һ�㣬����KQ��y���ڵ�G����M��KP��һ�㣬����MF��KF������MFK����PKQ��MP��AE+![]() GN�����Q���꣮
GN�����Q���꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ�����ı���ABCD�У�AB��CD���Խ���AC��BD���ڵ�E����F�ڱ�AB�ϣ�����CF���߶�BE�ڵ�G��CG2=GEGD��
��1����֤����ACF=��ABD��
��2������EF����֤��EFCG=EGCB��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
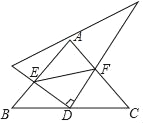
����Ŀ����ͼ����һ�����ǰ��к���30���ǵ����ǰ��ֱ�Ƕ������ڵ���ֱ�������ε�б�ߵ��е�D�������Ƶ�D��ת����ֱ�����ǰ����ֱ�DZ߷ֱ��ڵ�E��F�����н��ۣ���DE=DF����S�ı���AEDF=S��BED+S��CFD����S��ABC=EF2����EF2=BE2+CF2��������ȷ�������_____��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com