
【题目】如图,△ABC中,已知AB=AC,D是AC上的一点,CD=9,BC=15,BD=12.

(1)证明:△BCD是直角三角形.
(2)求△ABC的面积.
【答案】(1)证明见解析;(2)△ABC的面积为75.
【解析】
(1)由勾股定理逆定理可以证明△BCD是直角三角形;(2)要求△BCD的面积,已知BD的长度,即要求AC的长度,已知CD的长度,即要求AD的长度,设AD=x,根据勾股定理列方程求解.
(1)证明:∵ CD=9,BD=12,
∴ CD2+BD2=92+122=225,
∵ BC=15,∴ BC2=225,
∴ CD2+BD2=BC2,
∴ △BCD是直角三角形,且∠BDC=90°;
(2)设AD=x,则AC=x+9,
∵ AB=AC,∴ AB=x+9,
∵ ∠BDC=90°,∴ ∠ADB=90°,
∴ AB2=AD2+BD2,
∴ ![]() ,
,
解得:x=![]() ,
,
∴AC=![]() +9=
+9=![]() ,
,
∴S△ABC=![]() AC×BD=
AC×BD=![]() ×
×![]() ×12=75,
×12=75,
∴ △ABC的面积为75.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地. 如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系式;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.
下几种说法:
①货车的速度为60千米/小时;
②轿车与货车相遇时,货车恰好从甲地出发了3. 9小时;
③若轿车到达乙地后,马上沿原路以CD段速度返回,则轿车从乙地出发![]() 小时再次与货车相遇;
小时再次与货车相遇;
其中正确的个数是_________. (填写序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
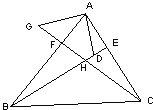
【题目】如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.
(1)求证:AD=AG;
(2)AD与AG的位置关系如何,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据以下10个乘积,回答问题:
![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;
![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;
(1)试将以上各乘积分别写成一个平方差的形式,并写出其中一个的思考过程
(2)将以上10个乘积按照从小到大排列起来
(3)若用![]() ,
,![]() ,
,![]() ,....
,....![]() ,表示n个乘积,其中
,表示n个乘积,其中![]() 为正数,试由(1)(2)猜测一个一般性的结论。(不要求写证明)
为正数,试由(1)(2)猜测一个一般性的结论。(不要求写证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了考察冰川的融化状况,一支科考队在某冰川上设定一个以大本营O为圆心,半径为4km的圆形考察区域,线段P1P2是冰川的部分边界线(不考虑其它边界),当冰川融化时,边界线沿着与其垂直的方向朝考察区域平行移动,若经过n年,冰川的边界线P1P2移动的距离为s(km),并且s与n(n为正整数)的关系是s= ![]() n2﹣
n2﹣ ![]() n+
n+ ![]() .以O为原点,建立如图所示的平面直角坐标系,其中P1、P2的坐标分别为(﹣4,9)、(﹣13、﹣3).
.以O为原点,建立如图所示的平面直角坐标系,其中P1、P2的坐标分别为(﹣4,9)、(﹣13、﹣3). 
(1)求线段P1P2所在直线对应的函数关系式;
(2)求冰川边界线移动到考察区域所需的最短时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】班级准备召开主题班会,现从由3名男生和2名女生所组成的班委中,随机选取两人担任主持人,求两名主持人恰为一男一女的概率.(请用“画树状图”或“列表”等方法写出过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
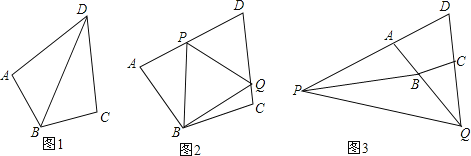
【题目】已知在四边形ABCD中,∠ABC+∠ADC=180°,AB=BC.
(1)如图1,若∠BAD=90°,AD=2,求CD的长度;
(2)如图2,点P、Q分别在线段AD、DC上,满足PQ=AP+CQ,求证:∠PBQ=90°![]() ∠ADC;
∠ADC;
(3)如图3,若点Q运动到DC的延长线上,点P也运动到DA的延长线上时,仍然满足PQ=AP+CQ,则(2)中的结论是否成立?若成立,请给出证明过程,若不成立,请写出∠PBQ与∠ADC的数量关系,并给出证明过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com