练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．某商品按进价的100%加价出售，经过一段时间，商家为减少库存，决定以7折销售，这时每件商品（　　）
    A．赚40%B．赔30%C．赔40%D．不赔不赚

    分析 设进价为x元，分别表示出原售价和新售价，并把新售价与进价比较，可得与进价的关系．

    解答 解：设进价为x元，则
    原售价为x×（1+100%）=2x，
    新售价为2x×0.7=1.4x元，
    1.4x-x=0.4x．
    这时每件商品的售价比进价多40%．
    故选：A．

    点评 此题考查一元一次方程的实际运用，解决问题的关键是读懂题意，找到关键描述语，找到所求的量的等量关系．要注意计算出新售价与进价比较．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    5．数学翻译  牛顿是举世闻名的伟大数学家、物理学家，他创立了微积分（另一个创立者是莱布尼茨）、经典力学，在代数学、光学、天文学等方面也作出了重要贡献，牛顿用数学的语言、方法描述和研究自然规律，他呕心沥血，写成的光辉著作《自然哲学的数学原理》，照亮了人类科学文明的大道，牛顿在他的《普遍的算术》一书中写道：“要解答一个含有数量间的抽象关系的问题，只要把题目由日常的语言译成代数的语言就行了．”下表是由牛顿给出的1个例子改写、简化而成的，请将表的空白补上（不必化简）．
    日常语言代数语言
    一个商人有一笔钱x
    第一年他花去了100镑x-100
    补进去余额的$\frac{1}{3}$（x-100）+$\frac{1}{3}$（x-100）
    第二年他又花去了100镑（1）（x-100）+$\frac{1}{3}$（x-100）-100
    又补进去余额的$\frac{1}{3}$（2）（x-100）+$\frac{1}{3}$（x-100）-100+$\frac{1}{3}$[（x-100）+$\frac{1}{3}$（x-100）-100]
    结果他的钱数正好是原来的钱数（3）（x-100）+$\frac{1}{3}$（x-100）-100+$\frac{1}{3}$[（x-100）+$\frac{1}{3}$（x-100）-100]=x
    根据上表中的（3）可解得x=400．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

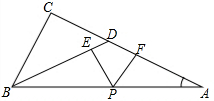    6．已知，如图，在△ABC中，∠C=90°，点D、P分别在边AC、AB上，且BD=AD，PE⊥BD，PF⊥AD，垂足分别为点E、F．
    （1）当∠A=30°时，求证：PE+PF=BC；
    （2）当A≠30°（∠A＜∠ABC）时，试问以上结论是否依然正确？如果正确，请加以证明；如果不正确，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图，△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P，若∠BPC=40°，求∠CAB的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．用下面方法确定$\sqrt{2}$的前面的几个小数位上的字．
    阅读理解：
    我们知道，正方形面积越大，其边长也越大，即如果两个正方形的面积分别为a、b，且a＜b，那么$\sqrt{a}＜\sqrt{b}$
    因为12＜2＜22，所以1＜$\sqrt{2}$＜2，可知$\sqrt{2}$的整数部分是1
    （1）取$\frac{1+2}{2}$=1.5，由1.52=2.25＞2，得1＜$\sqrt{2}$＜1.5
    （2）取$\frac{1+1.5}{2}=1.25，由1，2{5}^{2}$＜1.6＜2，得1.25＜$\sqrt{2}$＜1.5
    操作实践；
    继续像（1）、（2）那样取值和比较，确定$\sqrt{2}$的十分位和百分位上的数字．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如图中的图A是由10枚棋子组成的等边三角形图案，请你只移动三枚棋子变成图B的等边三角形图案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图，BD和CE是△ABC的角平分线．∠1=25°，∠2=20°，求∠A．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图，在长方形纸片ABCD中，AB=mAD，其中m≥1，将它沿EF折叠（点E、F分在边AB、CD上），使点B落在AD边上的点M处，点C落在点N处，若∠BEF=α，$\frac{AM}{EF}$的值（用含m，α的式子表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．已知线段AB的长为10cm，点C是线段AB的黄金分割点，且AC＞BC，则AC=5$\sqrt{5}$-5cm．（结果保留根号）

    查看答案和解析>>

    同步练习册答案