
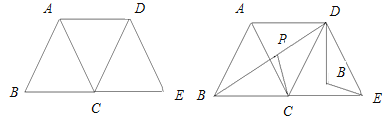
【题目】已知三个全等的等边三角形如图1所示放置,其中点B、C、E在同一直线上,
(1)写出两个不同类型的结论;
(2)连接BD,P为BD上的动点(D点除外),DP绕点D逆时针旋转60到DQ,如图2,连接PC,QE,
①判断CP与QE的大小关系,并说明理由;
②若等边三角形的边长为2,连接AP,在BD上是否存在点P,使AP+CP+DP的值最小,并求最小值.
【答案】(1)答案见解析;(2)①CP=QE,理由见解析;②存在,AP+CP+DP的最小值为![]()
【解析】解:(1)答案不唯一,合理即可,
如AD∥BE,四边形ABCD、ACED是菱形;
四边形ABED是等腰梯形;四边形ABED是轴对称图形;
 (2)①CP=QE;理由:
(2)①CP=QE;理由:
∵△AEC是等边三角形,
∴CD=DE,∠CDE=60,
∵DP绕点D逆时针旋转60到DQ,
∴PD=DQ,∠PDQ=60,
∴∠PDQ=∠QDE,
∴△DPC≌△DQE
∴CP=QE。
②连接AP,由①可知CP=QE,
∵DP绕点D逆时针旋转60到DQ,
∴△DPQ是等边三角形,
∴DP=DQ,
要使AP+CP+DP的值最小,关键是AP+QE+QP的值最小,即点A、P、Q、E在同一直线上(AE),构建两点之间,线段最短,过点A作AM⊥BE于点M,可得BM=1,EM=3,AM=![]() ,
,
所以AE=![]() ,
,
故在BD上存在点P,故AP+CP+DP的值最小,最小值是![]() .
.


科目:初中数学 来源: 题型:
【题目】对于一次函数y=x+2,下列结论中正确的是( )
A. 函数的图象与x轴交点坐标是(0,﹣2)
B. 函数值随自变量的增大而减小
C. 函数的图象向上平移2个单位长度得到函数y=x的图象
D. 函数的图象不经过第四象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一副直角三角板(其中一个三角板的内角是45°,45°,90°,另一个是30°,60°,90°)
(1)如图①放置,AB⊥AD,∠CAE=_______,BC与AD的位置关系是__________;
(2)在(1)的基础上,再拿一个30°,60°,90°的直角三角板,如图②放置,将AC′边和AD边重合, AE是∠CAB′的角平分线吗,如果是,请加以说明,如果不是,请说明理由.
(3)根据(1)(2)的计算,请解决下列问题:
如图③∠BAD=90°,∠BAC=∠FAD= ![]() (
(![]() 是锐角),将一个45°,45°,90°直角三角板的一直角边与AD边重合,锐角顶点A与∠BAD的顶点重合,AE是∠CAF的角平分线吗?如果是,请加以说明,如果不是,请说明理由.
是锐角),将一个45°,45°,90°直角三角板的一直角边与AD边重合,锐角顶点A与∠BAD的顶点重合,AE是∠CAF的角平分线吗?如果是,请加以说明,如果不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算①(x3)3=x6 ②a6·a4=a24 ③(ab4)4=ab8 ④2x2+5x2=7x2错误的是( )
A. ① ④B. ②③C. ①②D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
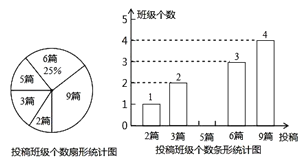
【题目】我市某校在八,九年级开展征文活动,校学生会对这两个年级各班内的投稿情况进行统计,并制成了如图所示的两幅不完整的统计图.
(1)求扇形统计图中投稿篇数为2所对应的扇形的圆心角的度数:
(2)求该校八,九年级各班在这一周内投稿的平均篇数,并将该条形统计图补充完整.
(3)在投稿篇数为9篇的4个班级中,八,九年级各有两个班,校学生会准备从这四个中选出两个班参加全市的表彰会,求出所选两个班正好不在同一年级的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com