
【题目】如图,![]() 是半径为1的
是半径为1的![]() 的内接正十边形,
的内接正十边形,![]() 平分
平分![]()
(1)求证:![]() ;
;
(2)求证:![]()
【答案】(1)详见解析;(2)详见解析
【解析】
(1)根据题意得出角相等得出△A1A2P∽△A1OA2,再根据相似三角形的性质即可得出答案;
(2)设A1A2=x,得出OP=PA2=A1A2=x,A1 P=1-x,再代入![]() 中即可求出答案.
中即可求出答案.
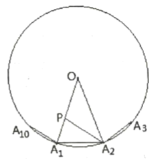
证明:(1)∵A1A2A3…A10是半径为1的⊙O的内接正十边形,A2P平分∠OA2A1
∴∠A1OA2=36°,∠A1=∠OA2A1=72°,∠A1A2P=∠O=36°
∴∠A1 P A2=72°,OP=PA2,
∴△A1A2P∽△A1OA2,![]()
∴A1A22=A1PO A1
(2)设A1A2=x,
则OP=PA2=A1A2=x,
∴A1 P=1-x,
由(1)得A1A22=A1PO A1
∴![]() ,
,
∴![]() ,
,
解得, (负值舍去)
(负值舍去)
∴![]() ,
,
即![]()


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】某市水费采用阶梯收费制度,即:每月用水不超过15吨时,每吨需缴纳水费a元,每月用水量超过15吨时,超过15吨的部分按每吨提高b元缴纳下表是嘉琪家一至四月份用水量和缴纳水费情况.根据表格提供的数据,回答:
月份 | 一 | 二 | 三 | 四 |
月用水量(吨) | 14 | 18 | 16 | 13 |
水费(元) | 42 | 60 | 50 | 39 |
(1)a= 元;b= 元;
(2)求月缴纳水费p(元)与月用水量t(吨)之间的函数关系式;
(3)若嘉琪家五月和六月的月缴水费相差24元,求这两月用水量差的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
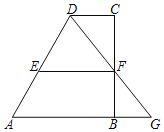
【题目】如图,四边形ABCD中,AB∥CD,CD≠AB,点F在BC上,连DF与AB的延长线交于点G.
(1)求证:CFFG=DFBF;
(2)当点F是BC的中点时,过F作EF∥CD交AD于点E,若AB=12,EF=8,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
问题情境:
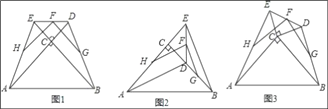
(1)如图1,两块等腰直角三角板△ABC和△ECD如图所示摆放,其中∠ACB=∠DCE=90°,点F,H,G分别是线段DE,AE,BD的中点,A,C,D和B,C,E分别共线,则FH和FG的数量关系是 ,位置关系是 .
合作探究:
(2)如图2,若将图1中的△DEC绕着点C顺时针旋转至A,C,E在一条直线上,其余条件不变,那么(1)中的结论还成立吗?若成立,请证明,若不成立,请说明理由.
(3)如图3,若将图1中的△DEC绕着点C顺时针旋转一个锐角,那么(1)中的结论是否还成立?若成立,请证明,若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某日王老师佩戴运动手环进行快走锻炼两次锻炼后数据如下表,与第一次锻炼相比,王老师第二次锻炼步数增长的百分率是其平均步长减少的百分率的![]() 倍.设王老师第二次锻炼时平均步长减少的百分率为
倍.设王老师第二次锻炼时平均步长减少的百分率为![]() .注:步数
.注:步数![]() 平均步长
平均步长![]() 距离.
距离.
项目 | 第一次锻炼 | 第二次锻炼 |
步数(步) |
| ①_______ |
平均步长(米/步) |
| ②_______ |
距离(米) |
|
|
(1)根据题意完成表格;
(2)求![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-4, 1),B(-1,3),C(-1,1)
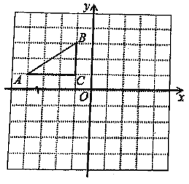
(1)将△ABC以原点O为旋转中心旋转180°,画出旋转后对应的△![]() ;平移△ABC,若A对应的点
;平移△ABC,若A对应的点![]() 坐标为(-4,-5),画出△
坐标为(-4,-5),画出△![]() ;
;
(2)若△![]() 绕某一点旋转可以得到△
绕某一点旋转可以得到△![]() ,直接写出旋转中心坐标是__________;
,直接写出旋转中心坐标是__________;
(3)在x轴上有一点P是的PA+PB的值最小,直接写出点P的坐标___________;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)一个不透明的口袋中装有2个红球(记为红球1、红球2)、1个白球、1个黑球,这些球除颜色外都相同,将球摇匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是 ;
(2)先从中任意摸出1个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表)求两次都摸到红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题呈现)阿基米德折弦定理:
如图1,AB和BC是⊙O的两条弦(即折线ABC是圆的一条折弦),BC>AB,点M是![]() 的中点,则从M向BC所作垂线的垂足D是折弦ABC的中点,即CD=DB+BA.下面是运用“截长法”证明CD=DB+BA的部分证明过程.
的中点,则从M向BC所作垂线的垂足D是折弦ABC的中点,即CD=DB+BA.下面是运用“截长法”证明CD=DB+BA的部分证明过程.
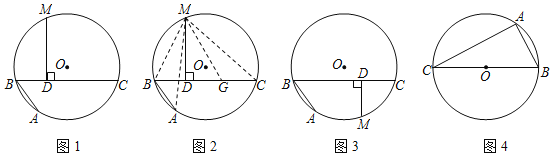
证明:如图2,在CD上截取CG=AB,连接MA、MB、MC和MG.
∵M是![]() 的中点,
的中点,
∴MA=MC①
又∵∠A=∠C②
∴△MAB≌△MCG③
∴MB=MG
又∵MD⊥BC
∴BD=DG
∴AB+BD=CG+DG
即CD=DB+BA
根据证明过程,分别写出下列步骤的理由:
① ,
② ,
③ ;
(理解运用)如图1,AB、BC是⊙O的两条弦,AB=4,BC=6,点M是![]() 的中点,MD⊥BC于点D,则BD= ;
的中点,MD⊥BC于点D,则BD= ;
(变式探究)如图3,若点M是![]() 的中点,(问题呈现)中的其他条件不变,判断CD、DB、BA之间存在怎样的数量关系?并加以证明.
的中点,(问题呈现)中的其他条件不变,判断CD、DB、BA之间存在怎样的数量关系?并加以证明.
(实践应用)根据你对阿基米德折弦定理的理解完成下列问题:
如图4,BC是⊙O的直径,点A圆上一定点,点D圆上一动点,且满足∠DAC=45°,若AB=6,⊙O的半径为5,求AD长.
查看答案和解析>>
科目:初中数学 来源: 题型:
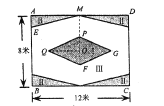
【题目】如图,某校准备给长12米,宽8米的矩形![]() 室内场地进行地面装饰,现将其划分为区域Ⅰ(菱形
室内场地进行地面装饰,现将其划分为区域Ⅰ(菱形![]() ),区域Ⅱ(4个全等的直角三角形),剩余空白部分记为区域Ⅲ;点
),区域Ⅱ(4个全等的直角三角形),剩余空白部分记为区域Ⅲ;点![]() 为矩形和菱形的对称中心,
为矩形和菱形的对称中心,![]() ,
,![]() ,
,![]() ,为了美观,要求区域Ⅱ的面积不超过矩形
,为了美观,要求区域Ⅱ的面积不超过矩形![]() 面积的
面积的![]() ,若设
,若设![]() 米.
米.
甲 | 乙 | 丙 | |
单价(元/米2) |
|
|
|
(1)当![]() 时,求区域Ⅱ的面积.
时,求区域Ⅱ的面积.
(2)计划在区域Ⅰ,Ⅱ分别铺设甲,乙两款不同的深色瓷砖,区域Ⅲ铺设丙款白色瓷砖,
①在相同光照条件下,当场地内白色区域的面积越大,室内光线亮度越好.当![]() 为多少时,室内光线亮度最好,并求此时白色区域的面积.
为多少时,室内光线亮度最好,并求此时白色区域的面积.
②三种瓷砖的单价列表如下,![]() 均为正整数,若当
均为正整数,若当![]() 米时,购买三款瓷砖的总费用最少,且最少费用为7200元,此时
米时,购买三款瓷砖的总费用最少,且最少费用为7200元,此时![]() __________,
__________,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com