【题目】计算：
（1）﹣0.5+3
+2.6﹣5
+1.15；
（2）﹣81÷|﹣2|×
÷（﹣16）；
（3）（﹣2）3+（﹣1）2÷
+（
）×（﹣18）．
一线名师权威作业本系列答案科目：初中数学 来源： 题型：
【题目】如图，△ABC三个顶点A（－3，5），B（－3，0），C（2，0），将△ABC绕点B顺时针旋转使A落在y轴上，与此同时顶点C恰好落在
的图象上，则k的值为( ）
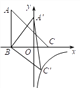
A. －2 B. －3 C. －4 D. －5
查看答案和解析>>
科目：初中数学 来源： 题型：
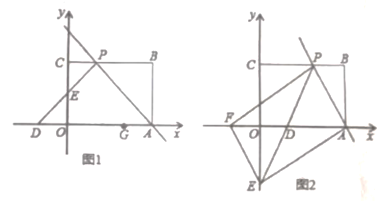
【题目】如图1，矩形
摆放在平面直角坐标系中，点
在
轴上，点
在
轴上，
，
，过点的直线交矩形的边
于点
，且点不与点
、重合，过点作
，
交轴于点
，交轴于点
．
（1）若
为等腰直角三角形．
①求直线
的函数解析式；
②在轴上另有一点
的坐标为
，请在直线和轴上分别找一点
、
，使
的周长最小，并求出此时点的坐标和周长的最小值．
（2）如图2，过点作
交轴于点
，若以、、、为顶点的四边形是平行四边形，求直线
的解析式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】周末，小李乘坐汽车从上海出发区苏州探望奶奶，全程88千米；返回时，因为另选了行车路线，全程为74千米。已知小李去时的平均速度是返回的1.1倍，所用时间却比返回时多了5分钟，求小李返回时所乘汽车的平均速度。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小刘对本班同学的业余兴趣爱好进行了一次调查，她根据采集到的数据，绘制了下面的图1和图2．
请你根据图中提供的信息，解答下列问题：
（1）在图1中，将“书画”部分的图形补充完整；
（2）在图2中，求出“球类”部分所对应的圆心角的度数，并分别写出爱好“音乐”、“书画”、“其它”的人数占本班学生数的百分数；
（3）观察图1和图2，你能得出哪些结论（只要写出一条结论）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一次函数
的图像过点
和点
，以线段
为边在第一象限内作等腰直角△ABC，使
（1）求一次函数的解析式；
（2）求出点
的坐标
（3）点
是
轴上一动点，当
最小时，求点的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，∠AOB＝120°，射线OP以1°/秒的速度从OA出发，射线OQ以2°/秒的速度从OB出发，两条射线同时开始逆时针转动t秒．
（1）当t＝10秒时，求∠POQ的度数．
（2）如图2，在射线OQ、OP转动过程中，射线OE始终在∠BOQ内部，且OF平分∠AOP，若∠EOF＝120°，求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，
，并且
满足
.一动点
从点
出发，在线段
上以每秒
个单位长度的速度向点
移动；动点
从点
出发在线段
上以每秒
个单位长度的速度向点
运动，点
分别从点
同时出发，当点运动到点时，点随之停止运动.设运动时间为
(秒)
(1)求
两点的坐标；
(2)当为何值时，四边形
是平行四边形？并求出此时两点的坐标.
(3)当为何值时，
是以
为腰的等腰三角形？并求出此时两点的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图 ，在平面直角坐标系中，直线AB∥ x轴，线段AB与 y 轴交于点M ，已知点 A的坐标是（－2，3）， BM4，点C 与点 B 关于 x 轴对称．
（1）在图中描出点C ，并直接写出点 B 和点C 的坐标：B ，C ；
（2）联结 AC 、BC ，AC 与 x 轴交于点 D ，试判断△ABC 的形状，并直接写出点 D的坐标；
（3）在坐标平面内， x 轴的下方，是否存在这样的点 P ，使得△ACP 是等腰直角三角形？如果存在，直接写出点P 的坐标；如果不存在，试说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
