Question

7．如图，在?ABCD中，AD⊥BD，AB=10，AD=6，以AD为斜边在?ABCD的内部作Rt△AED，使∠EAD=∠DBA，点A′、E′、D′分别与点A、E、D重合，△A′E′D′以每秒5个单位长度的速度沿DC方向平移，当点E′落在BC边上时停止移动，线段BD交边A′D′于点M，交边A′E′或D′E′于点N，设平移的时间为t（秒）．
（1）DM的长为4t（用含t的代数式表示）；
（2）当E′落在BD上时，求t的值；
（3）若△A′E′D′与△BDC重叠部分图形的面积为S（平方单位），求S与t之间的函数关系式；
（4）在不添加辅助线的情况下，直接写出平移过程中，出现于△DMD′全等的三角形时t的取值范围．

Answer 1

分析 （1）由△DMD′∽△BDA，得到$\frac{DM}{BD}$=$\frac{DD′}{AB}$=$\frac{MD′}{AD}$，由此即可解决问题．
（2）如图1中，当E′在BD上时，先证明DD′=D′E′，列出方程即可解决问题．
（3）分两种情形①当0＜t$≤\frac{18}{25}$时，如图2中，重叠部分是△D′MK，②当$\frac{18}{25}$＜t≤$\frac{32}{25}$时，如图3中，重叠部分是四边形D′E′KM，分别求解即可．
（4）分三种情形讨论即可：①当0＜t≤$\frac{18}{25}$时，如图2中，△DMD′≌△KMD′．②当DD′=D′C时，△DMD′≌△BMA′，③当DD′=AD时，△DMD′≌△AED．

解答 解：（1）∵AD⊥BD，
∴∠ADB=90°，
∴BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8，
∵AD∥A′D′，
∴A′D′⊥BD，
∴∠DMD′=∠ADB=90°，
∵CD∥AB，
∴∠D′DM=∠ABD，
∴△DMD′∽△BDA，
∴$\frac{DM}{BD}$=$\frac{DD′}{AB}$=$\frac{MD′}{AD}$，
∴$\frac{DM}{8}$=$\frac{5t}{10}$=$\frac{MD′}{6}$，
∴DM=4t，MD′=3t．
故答案为4t．

（2）如图1中，当E′在BD上时，

∵∠D′E′M+∠A′E′M=90°，∠MA′E′+∠A′E′M=90°，
∴∠E′A′M=∠D′E′M，
∵CD∥AB，
∴∠CDB=∠ABD，
∵∠E′A′M=∠ABD，
∴∠D′DE′=∠D′E′D，
∴DD′=D′E′，
由△ADE∽△BAD得到，DE=$\frac{18}{5}$，AE=$\frac{24}{5}$
∴5t=$\frac{18}{5}$，
∴t=$\frac{18}{25}$．

（3）①当0＜t$≤\frac{18}{25}$时，如图2中，重叠部分是△D′MK，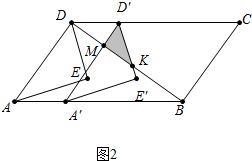

S=$\frac{1}{2}$D′M×MK=$\frac{1}{2}$×3t×4t=6t²．
②如图3中，过点E作JH∥AB，交AD于J，交BC于H，由题意可知，∠ADE=∠DJE，
∴EJ=ED=$\frac{18}{5}$，
∴EH=JH-EJ=10-$\frac{18}{5}$=$\frac{32}{5}$，
当$\frac{18}{25}$＜t≤$\frac{32}{25}$时，如图3中，重叠部分是四边形D′E′KM，

S=S_{△A′D′E′}-S_△A′MK=$\frac{1}{2}$×$\frac{18}{5}$×$\frac{24}{5}$-$\frac{1}{2}$（6-3t）•$\frac{3}{4}$（6-3t）=-$\frac{27}{8}$t²+$\frac{27}{2}$t-$\frac{263}{56}$．
综上所述S=$\left\{\begin{array}{l}{6{t}^{2}}&{（0＜t≤\frac{18}{25}）}\\{-\frac{27}{8}{t}^{2}+\frac{27}{2}t-\frac{263}{56}}&{（\frac{18}{25}＜t≤\frac{32}{25}）}\end{array}\right.$．

（4）①当0＜t≤$\frac{18}{25}$时，如图2中，△DMD′≌△KMD′．
②当DD′=D′C时，△DMD′≌△BMA′，此时t=1，
③当DD′=AD时，△DMD′≌△AED，此时5t=6，t=$\frac{6}{5}$，
综上所述当0＜t$≤\frac{18}{25}$ 或t=1 或t=$\frac{6}{5}$s时，出现与△DMD′全等的三角形．

点评 本题考查四边形综合题、平移变换、相似三角形的判定和性质，解题的关键是学会正确画好图形，学会分类讨论，考虑问题要全面，不能漏解，属于中考压轴题．