练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．计算：-1-2+|-$\sqrt{2}$-$\sqrt{3}$|+（π-3.14）0-tan60°+$\sqrt{8}$．

    分析 原式利用零指数幂、负整数指数幂法则，特殊角的三角函数值，以及绝对值的代数意义化简，计算即可得到结果．

    解答 解：原式=-1+（$\sqrt{3}+\sqrt{2}$）+1-$\sqrt{3}$$+2\sqrt{2}$
    =3$\sqrt{2}$

    点评 此题考查了实数的运算，零指数幂、负整数指数幂，以及特殊角的三角函数值，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

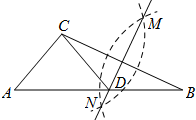    2．如图，在已知的△ABC中，按以下步骤作图：①分别以B、C为圆心，以大于$\frac{1}{2}$BC的长为半径作弧，两弧相交于点M、N；②作直线MN交AB于点D，连接CD，若CD=AD，∠B=20°，则下列结论中错误的是（　　）
    A．∠CAD=40°B．∠ACD=70°C．点D为△ABC的外心D．∠ACB=90°

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．7的相反数是（　　）
    A．7B．-7C．$\frac{1}{7}$D．-$\frac{1}{7}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．如图，∠ACD=120°，∠B=20°，则∠A的度数是（　　）
    A．120°B．90°C．100°D．30°

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．在平面直角坐标系中有一点A（-2，1），将点A先向右平移3个单位，再向下平移2个单位，则平移后点A的坐标为（1，-1）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．某校为了在九月份迎接高一年级的新生，决定将学生公寓楼重新装修．现学校招用了甲、乙两个工程队．若两队合作，8天就可以完成该项工程；若由甲队先单独做3天后，剩余部分由乙队单独做需要18天才能完成．
    （1）求甲、乙两队工作效率分别是多少？
    （2）甲队每天工资3000元，乙队每天工资1400元．学校要求在12天内将学生公寓楼装修完成．若完成该工程甲队工作m天，乙队工作n天．求学校需支付的总工资w（元）与甲队工作天数m（天）的函数关系式，并求出m的取值范围及w的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

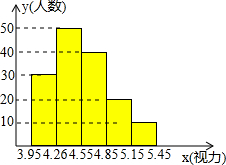    4．当今，青少年视力水平下降已引起了社会的关注，为了了解某校3000名学生的视力情况，从中抽取了一部分学生进行一次抽样调查，利用所得数据绘制的直方图（长方形的高表示该组人数）如图所示：
    解答下列问题：
    （1）本次抽样调查共抽测了多少名学生？
    （2）参加抽测学生的视力的众数在什么范围内？
    （3）若视力为4.85及以上为正常，试估计该校学生视力正常的人数约为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

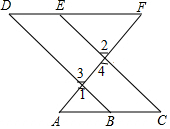    1．如图，点B在AC上，点E、D、F三点共线，∠2=∠1，∠FEC=∠DBA，把证明AC∥DF的过程补充完整．
    解：∵∠1=∠2（已知）
    且∠1=∠3（对顶角相等）
    ∴∠2=∠3（等量代换）
    ∴DB∥EC（同位角相等，两直线平行）
    ∴∠D=∠FEC（两直线平行，同位角相等）
    又∵∠FEC=∠DBA（已知）
    ∴∠D=∠DBA（等量代换）
    ∴AC∥DF（内错角相等，两直线平行）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．在平面直角坐标系xOy中，给出如下定义：
    对于⊙C及⊙C外一点P，M，N是⊙C上两点，当∠MPN最大时，称∠MPN为点P关于⊙C的“视角”．

    （1）如图，⊙O的半径为1，
    ①已知点A（0，2），画出点A关于⊙O的“视角”；
    若点P在直线x=2上，则点P关于⊙O的最大“视角”的度数60°；
    ②在第一象限内有一点B（m，m），点B关于⊙O的“视角”为60°，求点B的坐标．
    （2）若点P在直线y=-$\frac{\sqrt{3}}{3}$x+2上，且点P关于⊙O的“视角”大于60°，求点P的横坐标xP的取值范围．
    （3）⊙C的圆心在x轴上，半径为1，点E的坐标为（0，1），点F的坐标为（0，-1），若线段EF上所有的点关于⊙C的“视角”都小于120°，直接写出点C的横坐标xC的取值范围．

    查看答案和解析>>

    同步练习册答案