
【题目】某出租车司机从公司出发,在东西方向的人民路上连续接送5批客人,行驶路程记录如下(规定向东为正,向西为负,单位:km):
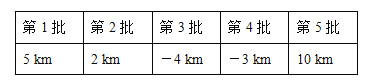
(1)接送完第5批客人后,该驾驶员在公司什么方向,距离公司多少千米?
(2)若该出租车每千米耗油0.2升,那么在这过程中共耗油多少升?
(3)若该出租车的计价标准为:行驶路程不超过3km收费10元,超过3km的部分按每千米加1.8元收费,在这过程中该驾驶员共收到车费多少元?
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】数学著作《算术研究》一书中,对于任意实数,通常用x 表示不超过 x 的最大整数,如 3 , 2 2 , 2.1 3 。给出如下结论:①x x ;②若x n ,则 x 的取值范围是 n x n 1 ;③当1 x 1 时, 1 x 1 x 的值为 1 或 2;④ x 2.75 是方程 4x 2x 5 0 的唯一一个解。其中正确的结论有( )
A.①②B.②③C.①③D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下表,回答问题:
x | … | -2 | -1 | 0 | 1 | 2 | … |
-2x+5 | … | 9 | 7 | 5 | 3 | a | … |
2x+8 | … | 4 | 6 | 8 | 10 | b | … |
(初步感知)
(1)a= ;b= ;
(归纳规律)
(2)随着x值的变化,两个代数式的值变化规律是什么?
(问题解决)
(3)比较-2x+5与2x+8的大小;
(4)请写出一个含x的代数式,要求x的值每增加1,代数式的值减小5,当x=0时,
代数式的值为-7.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验数据显示,一般成人喝半斤低度白酒后,1.5时内其血液中酒精含量y(毫克/百毫升)与时间x (时)的关系可近似地用二次函数y=-200x2+400x刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数![]() (k>0)刻画(如图所示).
(k>0)刻画(如图所示).
(1)根据上述数学模型计算:喝酒后几时血液中的酒精含量达到最大值?最大值为多少
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:30在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
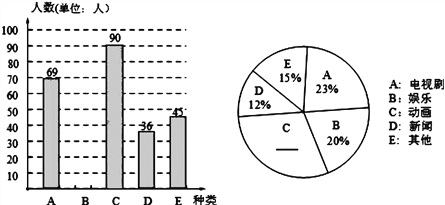
【题目】我市某中学为了了解本校学生对电视节目的喜爱情况,随机调查了部分学生最喜爱哪一类节目(被调查的学生只选一类并且没有不选择的),并将调查结果制成了如下的两个统计图(不完整).请你根据图中所提供的信息,完成下列问题:
(1)求本次调查的学生人数;
(2)请将两个统计图补充完整,并求出新闻节目在扇形统计图中所占圆心角的度数;
(3)若该中学有1500名学生,请估计该校喜爱电视剧节目的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知O为直线AD上一点,OB是∠AOC内部一条射线且满足∠AOB与∠AOC互补,OM,ON分别为∠AOC,∠AOB的平分线.

(1)∠COD与∠AOB相等吗?请说明理由;
(2)若∠AOB=30°,试求∠AOM与∠MON的度数;
(3)若∠MON=42°,试求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式;
(3)登山多长时间时,甲、乙两人距地面的高度差为70米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】育红学校七年级学生步行到郊外旅行.七(1)班的学生组成前队,步行速度为4km/h,七(2)班的学生组成后队,速度为6km/h.前队出发1h后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12km/h.
(1)当联络员追上前队时,离出发点多远?
(2)当联络员追上前队再到后队集合,总共用了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
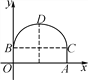
【题目】如图,东湖隧道的截面由抛物线和长方形构成,长方形的长OA为12 m,宽OB为4 m,隧道顶端D到路面的距离为10 m,建立如图所示的直角坐标系.
(1)求该抛物线的表达式;
(2)一辆货车载有一个长方体集装箱,集装箱最高处与地面距离为6 m,宽为4 m,隧道内设双向行车道,问这辆货车能否安全通过?
(3)在抛物线形拱壁上需要安装两排离地面高度相等的灯,如果灯离地面的高度不超过8.5 m,那么这两排灯的水平距离最小是多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com