
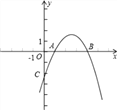
【题目】已知,抛物线y=ax2+bx-2与x轴的两个交点分别为A(1,0),B(4,0),与y轴的交点为C.
(1)求出抛物线的解析式及点C的坐标;
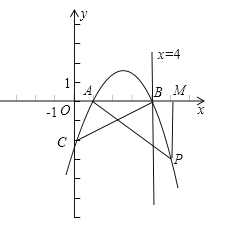
(2)点P是在直线x=4右侧的抛物线上的一动点,过P作PM⊥x轴,垂足为M,是否存在P点,使得以A,P,M为顶点的三角形与△OCB相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
【答案】(1)y=![]() x2+
x2+![]() x-2;(2)见解析
x-2;(2)见解析
【解析】试题分析:(1)由A和B两点在抛物线上,故把两点坐标代入抛物线解析式中,得到关于a与b的方程组,求出方程组的解即可得到a与b的值,从而确定出抛物线解析式,然后令求出的解析式中x=0,求出y的值即为C的纵坐标,写出C的坐标即可;
(2)存在P点,使得以A,P,M为顶点的三角形与△OCB相似,理由为:根据题意画出图形,如图所示,根据题意分别求出OA,OB及OC的长,设出P点的横坐标为m,代入抛物线解析式表示出纵坐标,因纵坐标为负值,求出其纵坐标的相反数即为PM的长,且用OM﹣OA表示出AM的长,若三角形相似,根据对应点对应不同分两种情况,由相似三角形对应边成比例列出关于m的方程,分别求出方程的解即可得到m的值,从而确定出P的坐标.
试题解析:解:(1)把A(1,0)和B(4,0)代入抛物线解析式得:
![]() ,②﹣①×4得:12a=﹣6,解得:a=﹣
,②﹣①×4得:12a=﹣6,解得:a=﹣![]() ,把a=﹣
,把a=﹣![]() 代入①,解得:b=
代入①,解得:b=![]() ,所以方程组的解为:
,所以方程组的解为: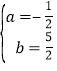 ,∴抛物线解析式为y=﹣
,∴抛物线解析式为y=﹣![]() x2+
x2+![]() x﹣2,令x=0,解得y=2,则C的坐标为(0,﹣2);
x﹣2,令x=0,解得y=2,则C的坐标为(0,﹣2);
(2)存在.根据题意画出图形,如图所示,设P的坐标为(m,﹣![]() m2+
m2+![]() m﹣2)(m>4),根据题意得:OA=1,OC=2,OB=4,则PM=
m﹣2)(m>4),根据题意得:OA=1,OC=2,OB=4,则PM=![]() m2﹣
m2﹣![]() m+2,MA=MO﹣OA=m﹣1,若△BOC∽△AMP,∴
m+2,MA=MO﹣OA=m﹣1,若△BOC∽△AMP,∴![]() =
=![]() ,即
,即![]() =
=![]() ,化简得:m2﹣6m+5=0,即(m﹣1)(m﹣5)=0,解得:m1=1(舍去),m2=5,则P坐标为(5,﹣2);
,化简得:m2﹣6m+5=0,即(m﹣1)(m﹣5)=0,解得:m1=1(舍去),m2=5,则P坐标为(5,﹣2);
若△BOC∽△PMA,∴![]() =
=![]() ,即
,即![]() =
=![]() ,化简得:m2﹣9m+8=0,即(m﹣1)(m﹣8)=0,解得:m1=1(舍去),m2=8,则P的坐标为(8,﹣14).
,化简得:m2﹣9m+8=0,即(m﹣1)(m﹣8)=0,解得:m1=1(舍去),m2=8,则P的坐标为(8,﹣14).
综上所述:满足题意的P有两个,其坐标分别为(5,﹣2)或(8,﹣14).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
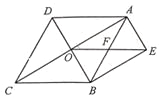
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,BE∥AC,AE∥BD,OE与AB交于点F.
(1)试判断四边形AEBO的形状,并说明理由;
(2)若OE=10,AC=16,求菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
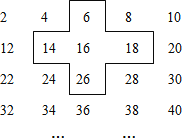
【题目】小明是个爱动脑筋的同学,在发现教材中的用方框在日历中移动的规律后,突发奇想,将连续的得数2,4,6,8,…,排成如图形式:并用一个十字形框架框住其中的五个数,请你仔细观察十字形框架中的数字的规律,并回答下列问题:
(1)请你选择十字框中你喜欢的任意位置的一个数,将其设为x,并用含x的代数式表示十字框中五个数的和.
(2)若将十字框上下左右移动,可框住另外的五个数,试间:十字框能否框住和等于2015的五个数,如能,请求出这五个数;如不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察如图所示的图形,回答下列问题:
(1)按甲方式将桌子拼在一起.
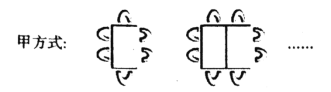
4张桌子拼在一起共有 个座位,n张桌子拼在一起共有 个座位;
(2)按乙方式将桌子拼在一起.
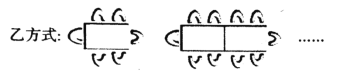
6张桌子拼在一起共有 个座位,m张桌子拼在一起共有 个座位;
(3)某食堂有A,B两个餐厅,现有102张这样的长方形桌子,计划把这些桌子全放在两个餐厅,每个餐厅都要放有桌子.将a张桌子放在A餐厅,按甲方式每6张拼成1张大桌子;将其余桌子都放在B餐厅,按乙方式每4张桌子拼成1张大桌子,若两个餐厅一共有404个座位,问A,B两个餐厅各有多少个座位?
查看答案和解析>>
科目:初中数学 来源: 题型:
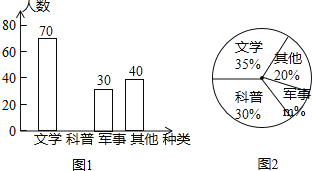
【题目】某学校在开展“书香校园”活动期间,对学生课外阅读的喜好进行抽样调查(每人只选一种书籍),将调查结果绘制成如图所示的两幅不完整的统计图,根据图中的信息,解答下列问题:
(1)这次调查的学生人数为 人,扇形统计图中m的值为 ;
(2)补全条形统计图;
(3)如果这所学校要添置学生课外阅读的书籍1500册,请你估计“科普”类书籍应添置多少册比较合适?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象与二次函数
的图象与二次函数![]() (
(![]() 为常数)的图象交于
为常数)的图象交于![]() 两点,且点
两点,且点![]() 的坐标为
的坐标为![]() .
.
(1)求出![]() 的值及点
的值及点![]() 的坐标;
的坐标;
(2)设![]() ,若
,若![]() 时,
时,![]() 随着
随着![]() 的增大而增大,且
的增大而增大,且![]() 也随着
也随着![]() 的增大而增大,求
的增大而增大,求![]() 的最小值和
的最小值和![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在点B的左边,线段AB的长为20cm;点C在点D的左边,点C、D在线段AB上,CD=10cm,点E是线段AC的中点,点F是线段BD的中点
(1)若AC=4cm,求线段EF的长;
(2)若AC=acm,![]() ,用含a的式子表示线段BF的长
,用含a的式子表示线段BF的长
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com