
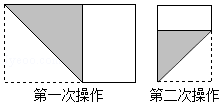
 长为1,宽为a的矩形纸片($\frac{1}{2}$<a<1),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n此操作后,剩下的矩形为正方形,则操作终止.当n=3时,求a的值.
长为1,宽为a的矩形纸片($\frac{1}{2}$<a<1),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n此操作后,剩下的矩形为正方形,则操作终止.当n=3时,求a的值. 分析 根据操作步骤,可知每一次操作时所得正方形的边长都等于原矩形的宽.所以首先需要判断矩形相邻的两边中,哪一条边是矩形的宽.当$\frac{1}{2}$<a<1时,矩形的长为1,宽为a,所以第一次操作时所得正方形的边长为a,剩下的矩形相邻的两边分别为1-a,a.由1-a<a可知,第二次操作时所得正方形的边长为1-a,剩下的矩形相邻的两边分别为1-a,a-(1-a)=2a-1.由于(1-a)-(2a-1)=2-3a,所以(1-a)与(2a-1)的大小关系不能确定,需要分情况进行讨论.又因为可以进行三次操作,故分两种情况:①1-a>2a-1;②1-a<2a-1.对于每一种情况,分别求出操作后剩下的矩形的两边,根据剩下的矩形为正方形,列出方程,求出a的值.
解答 解:由题意,可知当$\frac{1}{2}$<a<1时,第一次操作后剩下的矩形的长为a,宽为1-a,所以第二次操作时正方形的边长为1-a,第二次操作以后剩下的矩形的两边分别为1-a,2a-1.
故答案为:1-a;
此时,分两种情况:
①如果1-a>2a-1,即a<$\frac{2}{3}$,那么第三次操作时正方形的边长为2a-1.
∵经过第三次操作后所得的矩形是正方形,
∴矩形的宽等于1-a,
即2a-1=(1-a)-(2a-1),解得a=$\frac{3}{5}$;
②如果1-a<2a-1,即a>$\frac{2}{3}$,那么第三次操作时正方形的边长为1-a.
则1-a=(2a-1)-(1-a),解得a=$\frac{3}{4}$.
综上所述:a的值是$\frac{3}{5}$或$\frac{3}{4}$.
点评 本题考查了一元一次方程的应用,解题的关键是分两种情况:①1-a>2a-1;②1-a<2a-1.分别求出操作后剩下的矩形的两边.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
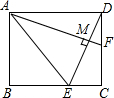 如图所示,在矩形ABCD中,F是DC上的一点,AE平分∠BAF交BC于点E,且DE⊥AF,垂足为点M,BE=3,AE=2$\sqrt{6}$,则MD的长是( )
如图所示,在矩形ABCD中,F是DC上的一点,AE平分∠BAF交BC于点E,且DE⊥AF,垂足为点M,BE=3,AE=2$\sqrt{6}$,则MD的长是( )| A. | $\sqrt{15}$ | B. | $\frac{{\sqrt{15}}}{15}$ | C. | 1 | D. | $\frac{{\sqrt{15}}}{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数y1=x+1的图象与x轴交于点A,与反比例函数y2=$\frac{k}{x}$的图象在第一象限内交于点B,作BC⊥x轴,垂足为C,且OC=1.
如图,一次函数y1=x+1的图象与x轴交于点A,与反比例函数y2=$\frac{k}{x}$的图象在第一象限内交于点B,作BC⊥x轴,垂足为C,且OC=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com