
【题目】如图,△ABC中,AB=AC=2,∠B=30°,点D在BC上,过点D作DE⊥BC,交BA或其延长线于点E,过点E作EF⊥BA交AC或其延长线于点F,连接DF.若DF⊥AC,则BD=_____.

【答案】![]()
【解析】分析:作AH⊥BC于H,如图,根据等腰三角形的性质得∠C=∠B=30°,BH=CH,再利用三角形外角性质得∠EAF=2∠B=60°,根据含30度角的直角三角形三边的关系得AH=![]() AB=1,BH=
AB=1,BH=![]() AH=
AH=![]() ,所以BC=2BH=2
,所以BC=2BH=2![]() ,同样可得AF=2AE,DF=
,同样可得AF=2AE,DF=![]() CD,CF=
CD,CF=![]() DF=
DF=![]() CD,设BD=x,则CD=2
CD,设BD=x,则CD=2![]() -x,在Rt△BDE中,根据含30度角的直角三角形三边的关系得DE=
-x,在Rt△BDE中,根据含30度角的直角三角形三边的关系得DE=![]() BD=
BD=![]() x,AE=2DE=
x,AE=2DE=![]() x,则AE=BE-AB=
x,则AE=BE-AB=![]() x-2,然后利用x表示出AF=
x-2,然后利用x表示出AF=![]() x-4,CF=
x-4,CF=![]() (2
(2![]() -x),最后利用AF+CF=AC列方程求解.
-x),最后利用AF+CF=AC列方程求解.
详解:作AH⊥BC于H,如图,

∵AB=AC=2,
∴∠C=∠B=30°,BH=CH,
∴∠EAF=2∠B=60°,AH=![]() AB=1,BH=
AB=1,BH=![]() AH=
AH=![]() ,
,
∴BC=2BH=2![]() ,
,
∵EF⊥AB,DF⊥AC,
∴∠AEF=90°,∠DFC=90°,
∴AF=2AE,DF=![]() CD,CF=
CD,CF=![]() DF=
DF=![]() CD,
CD,
设BD=x,则CD=2![]() -x,
-x,
在Rt△BDE中,DE=![]() BD=
BD=![]() x,
x,
∴BE=2DE=![]() x,
x,
∴AE=BE-AB=![]() x-2,
x-2,
∴AF=![]() x-4,CF=
x-4,CF=![]() (2
(2![]() -x),
-x),
∵AF+CF=AC,
∴![]() x-4+
x-4+![]() (2
(2![]() -x)=2,
-x)=2,
解得x=![]() ,
,
即BD的长为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】A、B两仓库分别有水泥20吨和30吨,C、D两工地分别需要水泥15吨和35吨.已知从A、B仓库到C、D工地的运价如下表:
到C工地 | 到D工地 | |
A仓库 | 每吨15元 | 每吨12元 |
B仓库 | 每吨10元 | 每吨9元 |
(1)若从A仓库运到C工地的水泥为![]() 吨,则用含x的代数式表示从A仓库运到D工地的水泥为 吨,从B仓库将水泥运到D工地的运输费用为 元;
吨,则用含x的代数式表示从A仓库运到D工地的水泥为 吨,从B仓库将水泥运到D工地的运输费用为 元;
(2)求把全部水泥从A、B两仓库运到C、D两工地的总运输费(用含![]() 的代数式表示并化简);
的代数式表示并化简);
(3)如果从A仓库运到C工地的水泥为15吨时,那么总运输费为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正五边形的边长为2,连接对角线AD,BE,CE,线段AD分别与BE和CE相交于点M,N,给出下列结论:①∠AME=108°;②![]() ;③MN=
;③MN=![]() ;④
;④![]() .其中正确结论的序号是________.
.其中正确结论的序号是________.
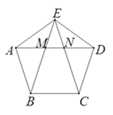
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上从左到右有![]() 三个点,点
三个点,点![]() 对应的数是10,
对应的数是10,![]() .
.
(1)点![]() 对应的数是________,点
对应的数是________,点![]() 对应的数是________.
对应的数是________.
(2)若数轴上有一点![]() ,且
,且![]() ,则点
,则点![]() 表示的数是什么?
表示的数是什么?
(3)动点![]() 从
从![]() 出发,以每秒4个单位长度的速度向终点
出发,以每秒4个单位长度的速度向终点![]() 移动,同时,动点
移动,同时,动点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度向终点
出发,以每秒1个单位长度的速度向终点![]() 移动,设移动时间为
移动,设移动时间为![]() 秒. 当点
秒. 当点![]() 和点
和点![]() 间的距离为8个单位长度时,求
间的距离为8个单位长度时,求![]() 的值.
的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点D、E分别是∠B的两边BC、BA上的点,∠DEB=2∠B,F为BA上一点.
(1)如图①,若DF平分∠BDE,求证:BD=DE+EF;
(2)如图②,若DF为△DBE的外角平分线,BD、DE、EF三者有怎样的数量关系?请证明你的结论.
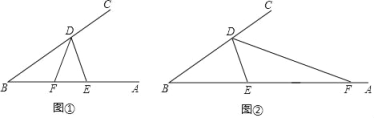
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的是( ).
A.在一个角的内部(包括顶点)到角的两边距离相等的点的轨迹是这个角的平分线
B.到点![]() 距离等于
距离等于![]() 的点的轨迹是以点
的点的轨迹是以点![]() 为圆心,半径长为
为圆心,半径长为![]() 的圆
的圆
C.到直线![]() 距离等于
距离等于![]() 的点的轨迹是两条平行于
的点的轨迹是两条平行于![]() 且与
且与![]() 的距离等于
的距离等于![]() 的直线
的直线
D.等腰三角形![]() 的底边
的底边![]() 固定,顶点
固定,顶点![]() 的轨迹是线段
的轨迹是线段![]() 的垂直平分线
的垂直平分线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有两点![]() 、
、![]() ,点
,点![]() 对应的数为-12,点
对应的数为-12,点![]() 在点
在点![]() 的右边,且距离
的右边,且距离![]() 点16个单位,点
点16个单位,点![]() 为数轴上一动点,其对应的数为
为数轴上一动点,其对应的数为![]() .
.
![]()
(1)若点![]() 到点
到点![]() ,
,![]() 的距离相等,求点
的距离相等,求点![]() 对应的数;
对应的数;
(2)是否存在这样的点![]() ,使点
,使点![]() 到点
到点![]() ,
,![]() 的距离之和为20?若存在,请求出
的距离之和为20?若存在,请求出![]() 的值;若不存在,请说明理由?
的值;若不存在,请说明理由?
(3)点![]() 是数轴上另一个动点,动点
是数轴上另一个动点,动点![]() ,
,![]() 分别从
分别从![]() ,
,![]() 同时出发,点
同时出发,点![]() 以每秒6个单位长度的速度沿数轴向右匀速运动,点
以每秒6个单位长度的速度沿数轴向右匀速运动,点![]() 以每秒4个单位长度的速度沿数轴向左匀速运动,点
以每秒4个单位长度的速度沿数轴向左匀速运动,点![]() 为
为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,且
上,且![]() ,设运动时间为
,设运动时间为![]() 秒.
秒.
①分别求数轴上点![]() ,
,![]() 表示的数(用含
表示的数(用含![]() 的式子表示);
的式子表示);
②![]() 为何值时,
为何值时,![]() ,
,![]() 之间的距离为10?
之间的距离为10?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为直线AB上一点,过点O作射线OC,将一直角三角板按图中所示的方式摆放(∠MON=900)
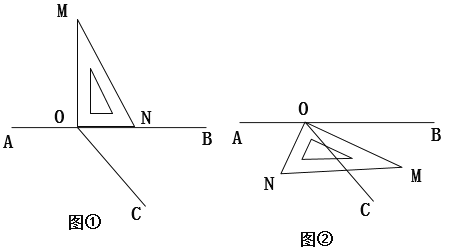
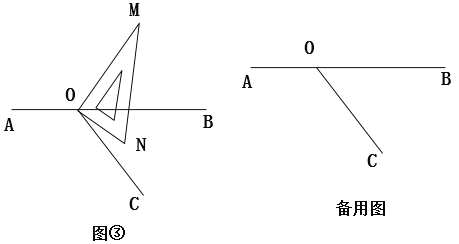
探究一:将图①中的三角板绕点0顺时针方向旋转一定的角度得到图②,使边OM恰好平分∠BOC。若∠BOC=500,ON是否平分∠A0C? 请说明理由;
探究二:将图①中的三角板绕点O时针旋转一定的角度得到图③,
(1)使边ON在∠BOC的内部,如果∠BOC=600,则∠BOM与∠CON之间存在怎样的数量关系?请说明理由。
(2)使边ON在∠BOC的内部,则∠BOM与∠NOC之间存在怎样的数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
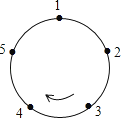
【题目】如图,圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5.若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,我们把这种走法称为一次“移位”.如:小明在编号为3的点,那么他应走3段弧长,即从3→4→5→1为第1次“移位”,这时他到达编号为1的点,那么他应走1段弧长,即从1→2为第2次“移位”.若小明从编号为4的点开始,第2019次“移位”后,他到达编号为_____的点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com