
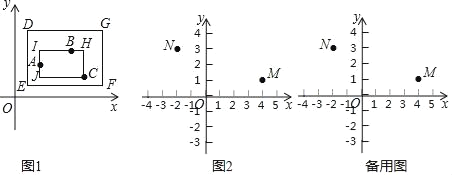
【题目】平面直角坐标系xOy中,对于任意的三个点A、B、C,给出如下定义:若矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的“三点矩形”.在点A,B,C的所有“三点矩形”中,若存在面积最小的矩形,则称该矩形为点A,B,C的“最佳三点矩形”.
如图1,矩形DEFG,矩形IJCH都是点A,B,C的“三点矩形”,矩形IJCH是点A,B,C的“最佳三点矩形”.
如图2,已知M(4,1),N(﹣2,3),点P(m,n).
(1)①若m=1,n=4,则点M,N,P的“最佳三点矩形”的周长为 ,面积为 ;
②若m=1,点M,N,P的“最佳三点矩形”的面积为24,求n的值;
(2)若点P在直线y=﹣2x+4上.
①求点M,N,P的“最佳三点矩形”面积的最小值及此时m的取值范围;
②当点M,N,P的“最佳三点矩形”为正方形时,求点P的坐标;
(3)若点P(m,n)在抛物线y=ax2+bx+c上,且当点M,N,P的“最佳三点矩形”面积为12时,﹣2≤m≤﹣1或1≤m≤3,直接写出抛物线的解析式.
【答案】(1)①18,18;②![]() 或5;(2)①最小值为12,
或5;(2)①最小值为12,![]() ;②点
;②点![]() 的坐标为
的坐标为![]() 或
或![]() ;(3)
;(3)![]() ,或
,或![]() .
.
【解析】
(1)①根据题意,易得M、N、P的“最佳三点矩形”的周长和面积②先求出![]() 和
和![]() 的值,再根据m=1以及M、N、P的“最佳三点矩形”的面积是24,可分析出此矩形的邻边长分别为6、4进而求出n的值
的值,再根据m=1以及M、N、P的“最佳三点矩形”的面积是24,可分析出此矩形的邻边长分别为6、4进而求出n的值
(2)①结合图形,易得M、N、P的“最佳三点矩形”的面积的最小值,分别将对应的值代入y=-2x+4即可求出m的取值范围②当M、N、P的“最佳三点矩形”为正方形时,易得边长为6,将对应的值代入y=-2x+4即可求出P点坐标
(3)根据题意画出图像,易得抛物线的解析式
解:(1)①如图,过P做直线AB平行于x轴,过N做直线AC平行于y轴,过M做MB平行于y轴,分别交于点A(-2,4)、C(-2,1)、B(4,1)

则AC=BM=3,AB=CM=6故周长=(3+6)![]() =18,面积=3
=18,面积=3![]() =18
=18
故M、N、P的“最佳三点矩形”的周长和面积分别为18,18;
② ∵M(4,1),N(-2,3)∴![]() ,
,![]()
又∵m=1,点M、N、P的“最佳三点矩形”的面积为24
∴此矩形的邻边长分别为6,4
∴n=-1或5
(2)如图1,
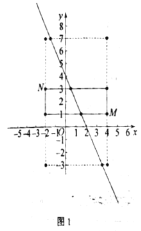
① 易得点M、N、P的“最佳三点矩形”的面积的最小值为12;
分别将y=3,y=1代入y=-2x+4,可得x分别为![]() ,
,![]()
结合图象可知:
②当点M、N、P的“最佳三点矩形”为正方形,边长为6,
分别将y=7,y=-3代入y=-2x+4 ,可得![]() 分别为
分别为![]() ,
,![]()
![]() 点P的坐标为(
点P的坐标为(![]() ,7)或(
,7)或(![]() ,-3)
,-3)
(3)如图2,y=![]() +
+![]() 或y=
或y=![]() +
+![]()


 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
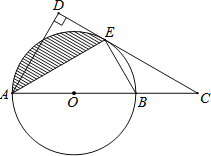
【题目】如图,AB是⊙O的直径,C是AB延长线上一点,CD与⊙O相切于点E,AD⊥CD于点D.
(1)求证:AE平分∠DAC;
(2)若AB=4,∠ABE=60°,求出图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P( x, y1)与Q (x, y2)分别是两个函数图象C1与C2上的任一点. 当a ≤ x ≤ b时,有-1 ≤ y1 - y2 ≤ 1成立,则称这两个函数在a ≤ x ≤ b上是“相邻函数”,否则称它们在a ≤ x ≤ b上是“非相邻函数”.
例如,点P(x, y1)与Q (x, y2)分别是两个函数y = 3x+1与y = 2x - 1图象上的任一点,当-3 ≤ x ≤ -1时,y1 - y2 = (3x + 1) - (2x - 1) = x + 2,通过构造函数y = x + 2,并研究它在-3 ≤ x ≤ -1上的性质,得到该函数值的范围是-1 ≤ y ≤ 1,所以-1 ≤ y1 - y2 ≤ 1成立,因此这两个函数在-3 ≤ x ≤ -1上是“相邻函数”.
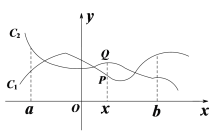
(1)判断函数y = 3x + 2与y = 2x + 1在-2 ≤ x≤ 0上是否为“相邻函数”,并说明理由;
(2)若函数y = x2 - x与y = x - a在0 ≤ x ≤ 2上是“相邻函数”,求a的取值范围;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,已知轮船甲在A处沿北偏东65°的方向匀速航行,同时轮船乙在轮船甲的南偏东40°方向的点B处沿某一方向航行,速度与甲轮船的速度相同.若经过一段时间后,两艘轮船恰好相遇,则轮船乙的航行方向为( )
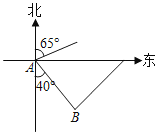
A.北偏西40°B.北偏东40°C.北偏西35°D.北偏东35°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正n边形的周长为60,边长为a
(1)当n=3时,请直接写出a的值;
(2)把正n边形的周长与边数同时增加7后,假设得到的仍是正多边形,它的边数为n+7,周长为67,边长为b.有人分别取n等于3,20,120,再求出相应的a与b,然后断言:“无论n取任何大于2的正整数,a与b一定不相等.”你认为这种说法对吗?若不对,请求出不符合这一说法的n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬遵义红色文化,传承红色文化精神,某校准备组织学生开展研学活动.经了解,有A.遵义会议会址、B.苟坝会议会址、C.娄山关红军战斗遗址、D.四渡赤水纪念馆共四个可选择的研学基地.现随机抽取部分学生对基地的选择进行调查,每人必须且只能选择一个基地.根据调查结果绘制如下不完整的条形统计图和扇形统计图.
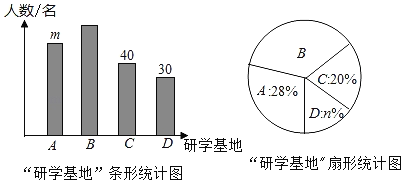
(1)统计图中m= ,n= ;
(2)若该校有1500名学生,请估计选择B基地的学生人数;
(3)某班在选择B基地的4名学生中有2名男同学和2名女同学,需从中随机选出2名同学担任“小导游”,请用树状图或列举法求这2名同学恰好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
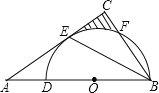
【题目】如图,△ABC中,BE是它的角平分线,∠C=90°,D在AB边上,以DB为直径的半圆O经过点E,交BC于点F.
(1)求证:AC是⊙O的切线;
(2)已知∠A=30°,⊙O的半径为4,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.

(1)求证:BG=DE;
(2)若E为AD中点,FH=2,求菱形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年9月30日,由著名导演李仁港执导的电影《攀登者》在各大影院上映后,好评不断,小亮和小丽都想去观看这部电影,但是只有一张电影票,于是他们决定采用模球的办法决定胜负,获胜者去看电影,游戏规则如下:在一个不透明的袋子中装有编号1-4的四个球(除编号外都相同),从中随机摸出一个球,记下数字后放回,再从中摸出一个球,记下数字,若两次数字之和大于5,则小亮获胜,若两次数字之和小于5,则小丽获胜.
(1)请用列表或画树状图的方法表示出随机摸球所有可能的结果;
(2)分别求出小亮和小丽获胜的概率,并判断这种游戏规则对两人公平吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com