
【题目】阅读材料,并回答问题
如图,有一根木棒 MN 放置在数轴上,它的两端 M、N 分别落在点 A、B.将木 棒在数轴上水平移动,当点 M 移动到点 B 时,点 N 所对应的数为 20,当点 N 移动到点 A 时,点 M 所对应的数为 5.(单位:cm)
![]()
由此可得,木棒长为 cm. 借助上述方法解决问题:
一天,美羊羊去问村长爷爷的年龄,村长爷爷说:“我若是你现在这么大,你还 要 40 年才出生呢,你若是我现在这么大,我已经是老寿星了,116 岁了,哈哈!” 美羊羊纳闷,村长爷爷到底是多少岁? 请你画出示意图,求出村长爷爷和美羊羊现在的年龄,并说明解题思路.
【答案】(1)5;(2)美羊羊今年12岁,村长爷爷今年64岁
【解析】试题分析:(1)由数轴观察知三根木棒长是20-5=15(cm),则此木棒长为5cm;(2)在求村长爷爷年龄时,借助数轴,把美羊羊与村长爷爷的年龄差看做木棒MN,类似村长爷爷比美羊羊大时看做当N点移动到A点时,此时M点所对应的数为-40,美羊羊比村长爷爷大时看做当M点移动到B点时,此时N点所对应的数为116,所以可知爷爷比小红大[116-(-40)]÷3=52,可知爷爷的年龄.
试题解析:(1)由数轴观察知三根木棒长是20﹣5=15,
则此木棒长为:15÷3=5,
故答案为:5.
(2)如图,
![]()
点A表示美羊羊现在的年龄,点B表示村长爷爷现在的年龄,木棒MN的两端分别落在点A、B.
由题意可知,当点N移动到点A时,点M所对应的数为﹣40,当点M移动到点B时,点N所对应的数为116.
可求MN=52.
所以点A所对应的数为12,点B所对应的数为64.
即美羊羊今年12岁,村长爷爷今年64岁.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:初中数学 来源: 题型:
【题目】如图所示,某公司有三个住宅区,A、B、C各区分别住有职工30人,15人,10人,且这三点在一条大道上(A,B,C三点共线),已知AB=100米,BC=200米.为了方便职工上下班,该公司的接送车打算在此间只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )
![]()
A. 点AB. 点BC. A,B之间D. B,C之间
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司开发出一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试营销,售价为8元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系,已知线段DE表示的函数关系中,时间每增加1天,日销售量减少5件. 
(1)第24天的日销售量是件,日销售利润是元.
(2)求y与x之间的函数关系式,并写出x的取值范围;
(3)日销售利润不低于640元的天数共有多少天?试销售期间,日销售最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化简并求值
(1)5x2y+[7xy﹣2(3xy﹣2x2y)﹣xy],其中x=﹣1,y=﹣![]()
(2)已知a2﹣a﹣2=0,求a2﹣2(a2﹣a+3)﹣![]() (a2﹣a﹣4)的值.
(a2﹣a﹣4)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx﹣8(a≠0)的对称轴是直线x=1,
(1)求证:2a+b=0;
(2)若关于x的方程ax2+bx﹣8=0,有一个根为4,求方程的另一个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,数轴上的点A,B,C,D表示的数分别为:-1.5,-3,2,3.5.
![]()
(1)将A,B,C,D表示的数按从小到大的顺序用“<”号连接起来;
(2)若将原点改在C点,其余各点所对应的数分别为多少?将这些数按从小到大的顺序用“<”连接起来;
(3)改变原点位置后,点A,B,C,D所表示的数大小顺序改变了吗?这说明了数轴的什么性质?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器超市销售每台进价分别为200元,170元的A,B两种型号的电风扇,表中是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A,B两种型号的电风扇的销售单价.
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,则A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
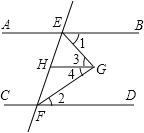
【题目】完成下面的证明:已知,如图,AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD,求证:∠EGF=90°
证明:∵HG∥AB(已知)
∴∠1=∠3
又∵HG∥CD(已知)
∴∠2=∠4
∵AB∥CD(已知)
∴∠BEF+ =180°
又∵EG平分∠BEF(已知)
∴∠1=![]() ∠
∠
又∵FG平分∠EFD(已知)
∴∠2=![]() ∠
∠
∴∠1+∠2=![]() ( )
( )
∴∠1+∠2=90°
∴∠3+∠4=90° 即∠EGF=90°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com