

| 三三角形角形 | 角的已知量 |  |  |
| 图2 | ∠A=2∠B=90° | ||
| 图3 | ∠A=2∠B=60° |
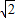 ,即可求得
,即可求得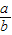 、
、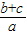 的值,图3的解法同上.
的值,图3的解法同上.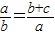 ,可通过构造相似三角形来证明;延长CA至D,是得AD=AB;那么∠CAB=2∠A=2∠CBA,再加上公共角∠C,即可证得△CBD∽△CAB,由此得到所求的结论.
,可通过构造相似三角形来证明;延长CA至D,是得AD=AB;那么∠CAB=2∠A=2∠CBA,再加上公共角∠C,即可证得△CBD∽△CAB,由此得到所求的结论.| 三角形 | 角的已知量 |  | 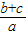 |
| 图2 | ∠A=2∠B=90° | 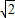 | 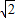 |
| 图3 | ∠A=2∠B=60° | 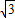 | 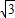 |
 延长CA至D,使AD=AB(如图4);
延长CA至D,使AD=AB(如图4);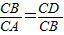 即
即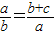 .(4分)
.(4分) ,解得c=-
,解得c=-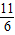 (不合题意舍去);
(不合题意舍去);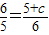 ,解得c=
,解得c=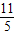 ;
;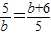 ,解得b=
,解得b=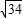 -3(负值舍去);
-3(负值舍去);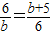 ,解得b=4(负值舍去);
,解得b=4(负值舍去);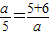 ,解得a=
,解得a=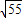 (负值舍去);
(负值舍去);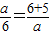 ,解得a=
,解得a=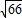 (负值舍去).
(负值舍去).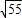 或
或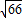 或
或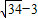 或4或
或4或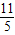 .
.

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
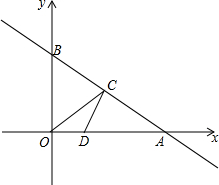 (2011•鞍山一模)如图,在平面直角坐标系中,直线y=-
(2011•鞍山一模)如图,在平面直角坐标系中,直线y=-
| ||
| 3 |
| 3 |
| ||
| 4 |
| ||
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com