
����Ŀ���й������������������߲�Ի�����2017��12��3���ڱ��������Ļ��ij����Ϊ�˽����Դ˴δ��Ĺ�ע�̶ȣ���ȫ������Χ�������ȡ���־�������ʾ����飬���ݵ��������Ѿ���Դ��Ĺ�ע�̶ȷֳ�������������һ����������ǿ��������ǿ���ĸ���Σ������Ƴ����������в�������ͳ��ͼ��
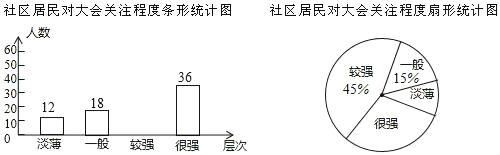
����������Ϣ������������⣺
��1����ε���һ����ȡ�˶���������
��2����ע�̶�Ϊ����ǿ���ľ���ռ��������������İٷֱ��Ƕ��٣�
��3���뽫����ͳ��ͼ����������
���𰸡���1����ε���ľ�������Ϊ120������2����ע�̶�Ϊ����ǿ���ľ���ռ��������������İٷֱ���30���� ��3����ȫ������ͳ��ͼ������.
��������
(1)���ݰ�ȫ��ʶһ�����18�ˣ���ռ�İٷֱ���15%���ݴ˼�����õ������������
(2)���ݰٷֱȵ����壬�ð�ȫ��ʶ��ǿ���������Ա���������������������ã�
(3)��������������ȫ��ʶ��ǿ��������ռ�İٷֱȼ�����⣬������ͼ��.
��1����ε���ľ�������Ϊ��18��15%=120���ˣ���
��2����ע�̶�Ϊ����ǿ���ľ���ռ��������������İٷֱ��ǣ�![]()
��3����ע�̶�Ϊ����ǿ���������ǣ�120��45%=54���ˣ�����ȫ������ͳ��ͼΪ��

�ʴ�Ϊ��(1)120����(2)30%��(3) ��ȫ������ͳ��ͼ������.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y= ![]() x��
x�� ![]() �����ABCO�ı�OC��BC�ֱ��ڵ�E��F����֪OA=3��OC=4�����CEF������ǣ�������
�����ABCO�ı�OC��BC�ֱ��ڵ�E��F����֪OA=3��OC=4�����CEF������ǣ�������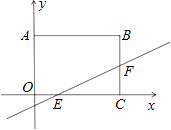
A.6
B.3
C.12
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��֪![]() ��
��![]() ��OMƽ��
��OMƽ��![]() ��ONƽ��
��ONƽ��![]() ��
��
(1)![]() ��
��
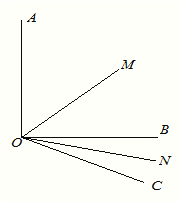
(2)��ͼ��AOB��900����OC��O��������ת��ʹ��BOC��![]() ����Ȼ�ֱ�����AOC����BOC��ƽ����OM��ON���ܷ������MON�Ķ��������ܣ������ֵ�������ܣ���˵�����ɣ�
����Ȼ�ֱ�����AOC����BOC��ƽ����OM��ON���ܷ������MON�Ķ��������ܣ������ֵ�������ܣ���˵�����ɣ�

(3)![]() ��
��![]() ����Ȼ�ֱ�����AOC����BOC��ƽ����OM��ON���ܷ������MON�Ķ��������ܣ���
����Ȼ�ֱ�����AOC����BOC��ƽ����OM��ON���ܷ������MON�Ķ��������ܣ���![]() �Ķ����������������п���ʲôʲô������
�Ķ����������������п���ʲôʲô������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ƽ��ֱ������ϵ�е�ԲO�İ뾶Ϊ3����������ʵ�飺����һö���ȵ������������ӣ������ĸ����㣬���������ֱ���1��2��3��4��ÿ�����㳯�ϵĻ�������ͬ�ģ������������Σ������ӳ��ϵĵ�����Ϊֱ������ϵ�е�P�����꣨��һ�εĵ���Ϊ�����꣬�ڶ��εĵ���Ϊ�����꣩�� 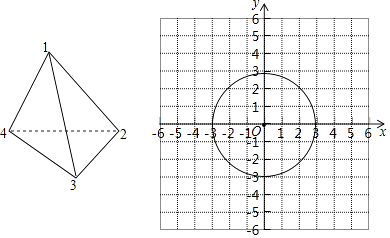
��1������һ�����ӳ��ϵĵ���Ϊ1���ڶ������ӳ��ϵĵ���Ϊ2����ʱ��P����ǡ�������ԲO�ڲ���
��2����������״ͼ���б��ķ�����ʾ��P����������п��ܽ����
��3�����P����ԲO���ϣ����ڲ���߽磩�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����������ĸ�������AB=DE��BC=EF����B=��E����C=��F��������ѡ����������ʹ��ABC����DEF�Ĺ��У�������

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�����������ͼ������ͼ������ͼ����ͼ��ʾ���ߴ絥λ�����ף�����һ��������������ͱ������д�������̣�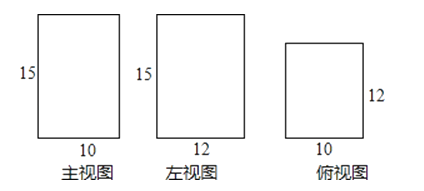
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(12��)���Ķ���������⣬�ٰ�Ҫ������������⣮
�����ⲻ��ʽ(x��2)(x��1)��0.
�⣺���������ij˷�������������ˣ�ͬ�ŵ�����������![]() ����
����![]()
�ⲻ��ʽ��������x��2.
�ⲻ��ʽ��������x����1.
���Բ���ʽ(x��2)(x��1)��0�Ľ⼯Ϊx��2��x����1.
�ⲻ��ʽ��(1)![]() ��0��(2)
��0��(2) ![]() ��0.
��0.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
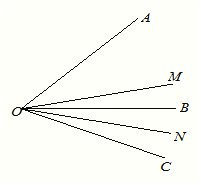
����Ŀ����ͼ����A +��B +��C +��D +��E +��F���ڣ� ��

A. 180�� B. 360�� C. 540�� D. 720��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ1����Rt��ABC�У���ACB=90�㣬��A=60�㣬CDƽ����ACB��
��֤��CA+AD=BC��
С��Ϊ��������������������˼��������ADC����ֱ��CD�ĶԳ�ͼ����A��DC��
��CDƽ����ACB����A��������CB�ϣ���CA��=CA��A��D=AD����ˣ�Ҫ֤������ת��ΪֻҪ֤A��D=A��B�������С����˼��д��������������֤�����̣�
��2�����գ�1����С����˼������������������⣺
��ͼ3�����ı���ABCD�У�ACƽ����BAD��BC=CD=10��AC=17��AD=9����AB�ij���

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com