
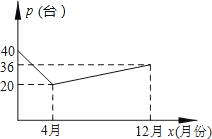
【题目】由于国家重点扶持节能环保产业,某种节能产品的销售市场逐渐回暖,某经销商销售这种产品,年初与生产厂家签订了一份进货合同,约定一年内进价为0.1万元/台.若一年内该产品的售价y(万元/台)与月份x(1≤x≤12且为整数)满足关系式:y=![]() ,一年后,发现这一年来实际每月的销售量p(台)与月份x之间存在如图所示的变化趋势.
,一年后,发现这一年来实际每月的销售量p(台)与月份x之间存在如图所示的变化趋势.
(1)求实际每月的销售量p(台)与月份x之间的函数表达式;
(2)全年中哪个月份的实际销售利润w最高,最高为多少万元?
【答案】(1)P=![]() ;(2)全年中1月份的实际销售利润w最高为8.75万元
;(2)全年中1月份的实际销售利润w最高为8.75万元
【解析】
(1)要根据自变量的不同取值范围,运用待定系数法分段计算出p与x的函数关系式;
(2)可根据实际销售利润=单件的利润×销售的数量,然后根据题目中给出的售价与月次的函数式以及(1)中销售量与月次的关系式,得出实际销售利润与月次的函数关系式,根据自变量的不同的取值范围分别进行讨论,然后找出最高售价.
(1)p=![]()
(2)①当1≤x<4时,
w=(﹣0.05x+0.4﹣0.1)×(﹣5x+40)
=![]() (x﹣6)(x﹣8)=
(x﹣6)(x﹣8)=![]() x2﹣
x2﹣![]() x+12
x+12
∵a=![]() >0,﹣
>0,﹣![]() =7>4,
=7>4,
∴当1≤x<4时,w随x的增大而减小,
∴当x=1时取得w的最大值为:
![]() ×12﹣
×12﹣![]() ×1+12=8.75 (万元).
×1+12=8.75 (万元).
②当4≤x≤12时,
w=(0.2﹣0.1)×(2x+12)=![]() x+
x+![]()
∵k=![]() >0,∴当4≤x≤12时,w随x的增大而增大,
>0,∴当4≤x≤12时,w随x的增大而增大,
∴当x=12时取得w的最大值为3.6:
![]() ×12+
×12+![]() =3.6 (万元).
=3.6 (万元).
综上得:全年中1月份的实际销售利润w最高为8.75万元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中有两点A(0,1),B(﹣1,0),动点P在反比例函数y=![]() 的图象上运动,当线段PA与线段PB之差的绝对值最大时,点P的坐标为_____.
的图象上运动,当线段PA与线段PB之差的绝对值最大时,点P的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,点E是AD的中点,连接BE,BF平分∠EBC交CD于点F,交AC于点G,将△CGF沿直线GF折叠至△C′GF,BD与△C′GF相交于点M、N,连接CN,若AB=6,则四边形CNC′G的面积是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与x轴交于点A,与反比例函数y=![]() (x>0)的图象交于点B(2,n),过点B作BC⊥x轴于点C,点P(3n﹣4,1)是该反比例函数图象上的一点,且∠PBC=∠ABC,求反比例函数和一次函数的表达式.
(x>0)的图象交于点B(2,n),过点B作BC⊥x轴于点C,点P(3n﹣4,1)是该反比例函数图象上的一点,且∠PBC=∠ABC,求反比例函数和一次函数的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
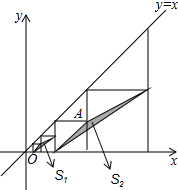
【题目】如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数![]() 的图象上,从左向右第3个正方形中的一个顶点A的坐标为
的图象上,从左向右第3个正方形中的一个顶点A的坐标为![]() ,阴影三角形部分的面积从左向右依次记为
,阴影三角形部分的面积从左向右依次记为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,则
,则![]() 的值为______
的值为______![]() 用含n的代数式表示,n为正整数
用含n的代数式表示,n为正整数![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+2x+m﹣2=0有两个实数根,m为正整数,且该方程的根都是整数,则符合条件的所有正整数m的和为( )
A. 6 B. 5 C. 4 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
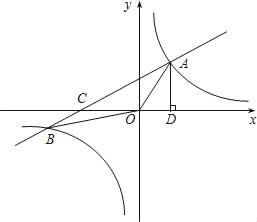
【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)与反比例函数y=![]() (m≠0)的图象相交于A、B两点,过点A作AD⊥x轴于点D,AO=5,OD=
(m≠0)的图象相交于A、B两点,过点A作AD⊥x轴于点D,AO=5,OD=![]() AD,B点的坐标为(﹣6,n).
AD,B点的坐标为(﹣6,n).
(1)求一次函数和反比例函数的表达式;
(2)P是y轴上一点,且△AOP是等腰三角形,请直接写出所有符合条件的P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
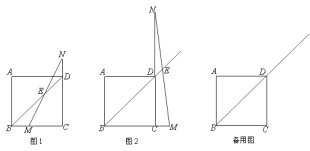
【题目】在正方形ABCD中,点M是射线BC上一点,点N是CD延长线上一点,且BM=DN.直线BD与MN相交于E.
(1)如图1,当点M在BC上时,求证:BD-2DE=![]() BM;
BM;
(2)如图2,当点M在BC延长线上时,BD、DE、BM之间满足的关系式是什么?;
(3)在(2)的条件下,连接BN交AD于点F,连接MF交BD于点G.若DE=![]() ,且AF:FD=1:2时,求线段DG的长.
,且AF:FD=1:2时,求线段DG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
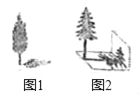
【题目】在“测量物体的高度”活动中,某数学兴趣小组的3名同学选择了测量学校里的两棵树的高度,在同一时刻的阳光下,他们分别做了以下工作:
小芳:测得一根长为1米的竹竿的影长为0.8米;
小丽:测量甲树的影长为4米(如图1);
小华:发现乙树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图2),墙壁上的影长为1.2米,落在地面上的影长为2.4米.
(1)请直接写出甲树的高度为 米;
(2)求乙树的高度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com