
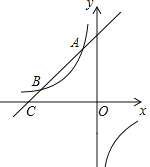
【题目】如图,一次函数y=x+b的图象与反比例函数y=![]() (k为常数且k≠0)的图象交于A(﹣1,a)、B两点,与x轴交于点C(﹣4,0).
(k为常数且k≠0)的图象交于A(﹣1,a)、B两点,与x轴交于点C(﹣4,0).
(1)求一次函数和反比例函数的表达式;
(2)若点D是第四象限内反比例函数图象上的点,且点D到直线AC的距离为5![]() ,求点D的横坐标.
,求点D的横坐标.
【答案】(1)y=x+4;y=﹣![]() ;(2)点D的横坐标x=±
;(2)点D的横坐标x=±![]() +3.
+3.
【解析】
(1)将点C坐标代入y=x+b可得其解析式,将A的坐标代入一次函数和反比例函数解析式可得k的值,从而得出反比例函数解析式;
(2)过点D作DE∥AC交x轴于点E,过点E作EF⊥AC于点F,设直线DE的解析式为y=x+m,EF=5![]() ,由题意得出CO=GO=4知CE=
,由题意得出CO=GO=4知CE=![]() EF=10,EO=6,从而得E(6,0),将E(6,0)代入y=x+m中得m=﹣6,从而得出y=x﹣6,联立
EF=10,EO=6,从而得E(6,0),将E(6,0)代入y=x+m中得m=﹣6,从而得出y=x﹣6,联立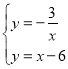 解之可得答案.
解之可得答案.
解:(1)将C(﹣4,0)代入y=x+b,得b=4,
∴一次函数的表达式为y=x+4,
将A(﹣1,a)代入y=x+4,y=![]() 中,得:a=﹣1+4,a=
中,得:a=﹣1+4,a=![]() ,
,
∴k=﹣3,
∴反比例函数的表达式为y=﹣![]() ;
;
(2)过点D作DE∥AC交x轴于点E,过点E作EF⊥AC于点F,
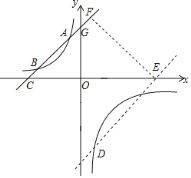
∴设直线DE的解析式为y=x+m,EF=5![]() ,
,
∵y=x+4,x=0时,y=4,
∴G(0,4),
又C(﹣4,0),
∴CO=GO=4,
又∠GOC=90°,
∴∠GCO=45°,
又∵EF⊥AC,
∴CE=![]() EF=10,
EF=10,
∴EO=EC-CO=6,
∴E(6,0),
将E(6,0)代入y=x+m中,得:m=﹣6,
∴y=x﹣6,
联立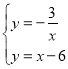 ,
,
解得x=![]() +3,
+3,
∴点D的横坐标为![]() +3或-
+3或-![]() +3.
+3.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某电器超市销售每台进价分别为2000元、1700元的A、B两种型号的空调,如表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 18000元 |
第二周 | 4台 | 10台 | 31000元 |
(进价、售价均保持不变,利润=销售总收入进货成本)
(1)求A、B两种型号的空调的销售单价;
(2)若超市准备用不多于54000元的金额再采购这两种型号的空调共30台,求A种型号的空调最多能采购多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
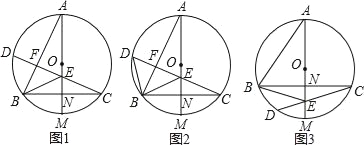
【题目】已知AM是⊙O直径,弦BC⊥AM,垂足为点N,弦CD交AM于点E,连按AB和BE.
(1)如图1,若CD⊥AB,垂足为点F,求证:∠BED=2∠BAM;
(2)如图2,在(1)的条件下,连接BD,若∠ABE=∠BDC,求证:AE=2CN;
(3)如图3,AB=CD,BE:CD=4:7,AE=11,求EM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点到直线的距离即为点到直线的垂线段的长.

(1)如图1,取点M(1,0),则点M到直线l:y=![]() x﹣1的距离为多少?
x﹣1的距离为多少?
(2)如图2,点P是反比例函数y=![]() 在第一象限上的一个点,过点P分别作PM⊥x轴,作PN⊥y轴,记P到直线MN的距离为d0,问是否存在点P,使d0=
在第一象限上的一个点,过点P分别作PM⊥x轴,作PN⊥y轴,记P到直线MN的距离为d0,问是否存在点P,使d0=![]() ?若存在,求出点P的坐标,若不存在,请说明理由.
?若存在,求出点P的坐标,若不存在,请说明理由.
(3)如图3,若直线y=kx+m与抛物线y=x2﹣4x相交于x轴上方两点A、B(A在B的左边).且∠AOB=90°,求点P(2,0)到直线y=kx+m的距离最大时,直线y=kx+m的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
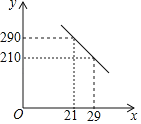
【题目】一名大学毕业生响应国家“自主创业”的号召,在成都市高新区租用了一个门店,聘请了两名员工,计划销售一种产品.已知该产品成本价是20元/件,其销售价不低于成本价,且不高于30元/件,员工每人每天的工资为200元.经过市场调查发现,该产品每天的销售量y(件)与销售价x(元/件)之间的函数关系如图所示.
(1)求y与x之间的函数关系式;
(2)求每件产品销售价为多少元时,每天门店的纯利润最大?最大纯利润是多少?(纯利润=销售收入﹣产品成本﹣员工工资)
查看答案和解析>>
科目:初中数学 来源: 题型:
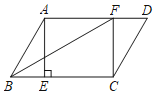
【题目】如图,ABCD中,点E,F分别在边BC,AD上,BE=DF,∠AEC=90°.
(1)求证:四边形AECF是矩形;
(2)连接BF,若AB=4,∠ABC=60°,BF平分∠ABC,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,∠ACB=90°,AC=BC=![]() ,M为BC边上的一个动点(不与点B,C重合),连接AM,以点A为中心,将线段AM逆时针旋转135°,得到线段AN,连接BN.
,M为BC边上的一个动点(不与点B,C重合),连接AM,以点A为中心,将线段AM逆时针旋转135°,得到线段AN,连接BN.

(1)依题意补全图2;
(2)求证:∠BAN=∠AMB;
(3)点P在线段BC的延长线上,点M关于点P的对称点为Q,写出一个PC的值,使得对于任意的点M,总有AQ=BN,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
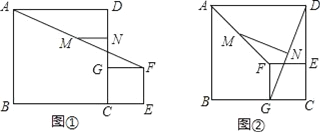
【题目】如图①,C为线段BE上的一点,分别以BC和CE为边在BE的同侧作正方形ABCD和正方形CEFG,M、N分别是线段AF和GD的中点,连接MN
(1)线段MN和GD的数量关系是_____,位置关系是_____;
(2)将图①中的正方形CEFG绕点C逆时针旋转90°,其他条件不变,如图②,(1)的结论是否成立?说明理由;
(3)已知BC=7,CE=3,将图①中的正方形CEFG绕点C旋转一周,其他条件不变,直接写出MN的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线L:y=kx+2k(k>0)与x轴交于点A,与y轴交于点B,与函数![]() (x>0)的图象的交点P位于第一象限.
(x>0)的图象的交点P位于第一象限.
(1)若点P的坐标为(1,6),
①求m的值及点A的坐标;
②![]() =_________;
=_________;
(2)直线h:y=2kx-2与y轴交于点C,与直线L1交于点Q,若点P的横坐标为1,
①写出点P的坐标(用含k的式子表示);
②当PQ≤PA时,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com