
【题目】如图,点A是线段DE上一点,∠BAC=90°,AB=AC,BD⊥DE,CE⊥DE.
(1)求证:DE=BD+CE.
(2)如果是如图2这个图形,BD、CE、DE有什么数量关系?并证明.

【答案】(1)见解析;(2)BD=DE+CE,理由见解析.
【解析】
(1)先证△AEC≌△BDA得出AD=CE,BD=AE,从而得出DE=BD+CE;
(2)先证△ADB≌△CEA得出AD=CE,BD=AE,从而得出BD=DE+CE.
(1)∵BD⊥DE,CE⊥DE,∴∠D=∠E=90°,∴∠DBA+∠DAB=90°.
∵∠BAC=90°,∴∠DAB+∠CAE=90°,∴∠DBA=∠CAE.
∵AB=AC,∴△ADB≌△CEA,∴BD=AE,CE=AD,∴DE=AD+AE=CE+BD;
(2)BD=DE+CE.理由如下:
∵BD⊥DE,CE⊥DE,∴∠ADB=∠AEC=90°,∴∠ABD+∠BAD=90°.
∵∠BAC=90°,∴∠ABD+∠EAC=90°,∴∠BAD=∠EAC.
∵AB=AC,∴△ADB≌△CEA,∴BD=AE,CE=AD.
∵AE=AD+DE,∴BD=CE+DE.


科目:初中数学 来源: 题型:
【题目】已知函数y=(m+1)x+2m-6.
(1)若函数图象过(-1,2),求此函数的解析式;
(2)若函数图象与直线y=2x+5平行,求其函数的解析式;
(3)求满足(2)条件的直线与直线y=-3x+1的交点,并求这两条直线与y轴所围成的三角形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工人师傅做铝合金窗框分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料(如图①),使AB=CD,EF=GH;
(2)摆放成如图②的四边形,则这时窗框的形状是______形,根据的数学原理是:_______________________;
(3)将直角尺靠紧窗框的一个角(如图③),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图④),说明窗框合格,这时窗框是_______形,根据的数学原理是:_____________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第1个等式:1-![]() =
=![]() ×
×![]()
第2个等式:(1-![]() )(1-
)(1-![]() )=
)=![]() ×
×![]()
第3个等式:(1-![]() )(1-
)(1-![]() )(1-
)(1-![]() )=
)=![]() ×
×![]()
第4个等式:(1-![]() )(1-
)(1-![]() )(1-
)(1-![]() )(1-
)(1-![]() )=
)=![]() ×
×![]()
第5个等式:(1-![]() )(1-
)(1-![]() )(1-
)(1-![]() )(1-
)(1-![]() )(1-
)(1-![]() )=
)=![]() ×
×![]()
······
(1) 写出第6个等式;
(2) 写出第n个等式(用含n的等式表示),并予以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA⊥OC,OB⊥OD,四位同学分别说了自己的观点.
甲:∠AOB=∠COD.
乙:∠BOC+∠AOD=180°.
丙:∠AOB与∠COD都是∠BOC的余角.
丁:图中小于平角的角有4个.
其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形ABC为一个电子跳蚤游戏盘,其中AB=8,AC=9,BC=10.如果电子跳蚤开始时在BC边上的点P0处,BP0=4,第一步跳蚤从点P0处跳到AC边上的点P1处,且CP1=CP0;第二步跳蚤从点P1处跳到AB边上的点P2处,且AP1=AP2;第三步跳蚤从点P2处跳回到BC边上的点P3处,且BP3=BP2……若跳蚤按上述规则跳下去,第n次的落点为Pn,则点P3与点P2019之间的距离为( )
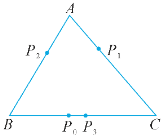
A. 0 B. 1 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.
(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,EF切⊙O于点D,过点B作BH⊥EF于点H,交⊙O于点C,连接BD. 
(1)求证:BD平分∠ABH;
(2)如果AB=12,BC=8,求圆心O到BC的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
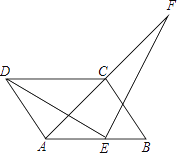
【题目】如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E是AB的中点,F是AC延长线上一点.
(1)若ED⊥EF,求证:ED=EF;
(2)在(1)的条件下,若DC的延长线与FB交于点P,试判定四边形ACPE是否为平行四边形?并证明你的结论(请先补全图形,再解答);
(3)若ED=EF,ED与EF垂直吗?若垂直给出证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com