
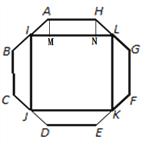
【题目】如图,正八边形ABCDEFGH的边长为a,I、J、K、L分别是各自所在边的中点,且四边形IJKL是正方形,则正方形IJKL的边长为________(用含a的代数式表示).

【答案】![]()
【解析】分析:过点A作AM⊥IL于点M,过点H作HN⊥IL与点N,可得四边形AMNH为矩形,根据正八边形的性质可得∠BAH=135°,由此可得∠BAM=45°,在等腰直角三角形AIM中,AI=![]() ,可求得AM=IM=
,可求得AM=IM=![]() ,同理求得HN=LN=
,同理求得HN=LN=![]() ,所以IL=IM+MN+LN=IM+AH+LN=
,所以IL=IM+MN+LN=IM+AH+LN=![]() +a+
+a+![]() =
=![]() .
.
详解:
过点A作AM⊥IL于点M,过点H作HN⊥IL与点N,可得四边形AMNH为矩形,
∵八边形ABCDEFGH为正八边形,
∴∠BAH=135°,
∵∠HAM=90°,
∴∠BAM=45°,
在等腰直角三角形AIM中,AI=![]()
∴AM=IM=![]() ;
;
同理求得HN=LN=![]() ,
,
∴IL=IM+MN+LN=IM+AH+LN=![]() +a+
+a+![]() =
=![]() .
.
故答案为:![]() .
.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.A、B、C三点在格点上.
(1)作出△ABC关于y轴对称的△A1B1C1,并写出点C1的坐标 ;
(2)在(1)的条件下,连接CC1交AB于点D,请标出点D,并直接写出CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菜农李伟种植的某蔬菜计划以每千克![]() 元的单价对外批发销售,由于部分菜农盲目扩大种植,造成该蔬菜滞销.李伟为了加快销售,减少损失,对价格经过两次下调后,以每千克
元的单价对外批发销售,由于部分菜农盲目扩大种植,造成该蔬菜滞销.李伟为了加快销售,减少损失,对价格经过两次下调后,以每千克![]() 元的单价对外批发销售.
元的单价对外批发销售.
![]() 求平均每次下调的百分率;
求平均每次下调的百分率;
![]() 小华准备到李伟处购买
小华准备到李伟处购买![]() 吨该蔬菜,因数量多,李伟决定再给予两种优惠方案以供选择:
吨该蔬菜,因数量多,李伟决定再给予两种优惠方案以供选择:
方案一:打九折销售;
方案二:不打折,每吨优惠现金![]() 元.
元.
试问小华选择哪种方案更优惠,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,M为AB中点.将△ACM沿CM翻折,得到△DCM(如图2),P为CD上一点,再将△DMP沿MP翻折,使得D与B重合(如图3),给出下列四个命题:
①BP∥AC;②△PBC≌△PMC;③PC⊥BM;④∠BPC=∠BMC.
其中真命题的个数是( )

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,矩形ABCD中,AB=4,BC=m(m>1),点E是AD边上一定点,且AE=1.
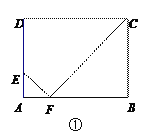
(1)当m=3时,AB上存在点F,使△AEF与△BCF相似,求AF的长度.
(2)如图②,当m=3.5时.用直尺和圆规在AB上作出所有使△AEF与△BCF相似的点F.(不写作法,保留作图痕迹)

(3)对于每一个确定的m的值,AB上存在几个点F,使得△AEF与△BCF相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E,AB=10,AC=6,求△ADE的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“8字”的性质及应用:
(1)如图1,AD、BC相交于点O,得到一个“8字”ABCD,求证:∠A+∠B=∠C+∠D.
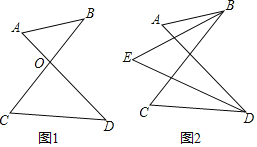
(2)如图2,∠ABC和∠ADC的平分线相交于点E,利用(1)中的结论证明:∠E=![]() (∠A+∠C).
(∠A+∠C).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF.
(1)求证:AD平分∠BAC;
(2)直接写出AB+AC与AE之间的等量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,正方形的中心在原点![]() ,且正方形的一组对边与
,且正方形的一组对边与![]() 轴平行.点
轴平行.点![]() 是反比例幽数
是反比例幽数![]() 的图象上与正方形的一个交点,若图中阴影部分的面积等于
的图象上与正方形的一个交点,若图中阴影部分的面积等于![]() ,则
,则![]() 的值为( )
的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com