
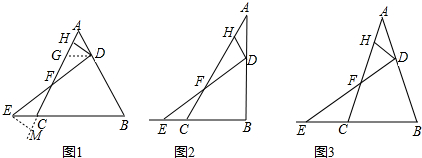
分析 (1)过点D作DG∥BC交AC于点G,由题意知△AGD是等边三角形,所以AD=GD,所以可以证明△GDF≌△CEF,所以CF=GF,由三线合一可知:AH=GH,所以$\frac{AC}{HF}=2$;
(2)过点D作DG∥BC交AC于点G,由点D,E的运动速度之比是$\sqrt{3}:1$可知GD=CE,所以可以证明△GDF≌△CEF,所以CF=GF,由∠ABC=90°,∠ADH=∠BAC=30°可知:AH=DH,所以$\frac{AC}{HF}=2$;
(3)类似(1)(2)的方法可求出$\frac{AH}{AG}=m$和$\frac{GF}{CF}$=m,然后利用GH+FG=m(AH+FC)=m(AC-HF)即可求出$\frac{AC}{HF}$的比值.
解答 解:(1)过点D作DG∥BC交AC于点G,
∵△ABC是等边三角形,
∴△AGD是等边三角形,
∴AD=GD,
由题意知:CE=AD,
∴CE=GD
∵DG∥BC,
∴∠GDF=∠CEF,
在△GDF与△CEF中,
$\left\{\begin{array}{l}{∠GDF=∠CEF}\\{∠GFD=∠EFC}\\{CE=GD}\end{array}\right.$,
∴△GDF≌△CEF(AAS),
∴CF=GF,
∵DH⊥AG,
∴AH=GH,
∴AC=AG+CG=2GH+2GF=2(GH+GF),
HF=GH+GF,
∴$\frac{AC}{HF}$=2;
(2)过点D作DG∥BC交AC于点G,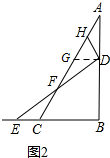
由题意知:点D,E的运动速度之比是$\sqrt{3}:1$
∴$\frac{AD}{CE}$=$\sqrt{3}$,
∵∠ABC=90°,∠BAC=30°,
∴$\frac{AD}{GD}$=$\sqrt{3}$,
∴$\frac{AD}{CE}=\frac{AD}{GD}$,
∴GD=CE,
∵DG∥BC,
∴∠GDF=∠CEF,
在△GDF与△CEF中,
$\left\{\begin{array}{l}{∠GDF=∠CEF}\\{∠GFD=∠EFC}\\{CE=GD}\end{array}\right.$,
∴△GDF≌△CEF(AAS),
∴CF=GF,
∵∠ADH=∠BAC=30°,
∴AH=HD,
∵∠AGD=∠HDG=60°,
∴GH=HD,
∴AH=HG,
∴AC=AG+CG=2GH+2GF=2(GH+GF),
HF=GH+GF,
∴$\frac{AC}{HF}$=2;
(3)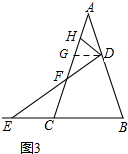 过点D作DG∥BC交AC于点G
过点D作DG∥BC交AC于点G
∵DG∥BC,
∴△AGD∽△ACB,
∴$\frac{GD}{AG}=\frac{BC}{AC}=m$,
∵∠ADH=∠BAC=36°,AC=AB,
∴∠GHD=∠HGD=72°,
∴GD=HD=AH,
∴$\frac{AH}{AG}=\frac{GD}{AG}=m$,
∵AD=CE,
∴$\frac{GD}{AD}=\frac{GD}{AG}$=$\frac{GD}{CE}$=m,
∵DG∥BC,
∴△DGF∽△ECF,
∴$\frac{GD}{CE}=\frac{GF}{CF}$=m,
∴GH+FG=m(AH+FC)=m(AC-HF),
即HF=m(AC-HF),
∴$\frac{AC}{HF}$=$\frac{m+1}{m}$.
点评 本题考查三角形的综合问题,涉及全等三角形的判定和性质,相似三角形的判定与性质,等边三角形的性质,直角三角形的性质等知识内容,内容比较综合,需要学生灵活运用所学的知识进行解答.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 月用水量 | 频数 |
| 0≤x<0.5 | 1 |
| 0.5≤x<1 | 2 |
| 1≤x<1.5 | 3 |
| 1.5≤x<2 | 4 |
| 2≤x<2.5 | 3 |
| 2.5≤x<3 | 3 |
| 3≤x<3.5 | 2 |
| 3.5≤x<4 | 1 |
| 4≤x<4.5 | 1 |
| A. | 0.15 | B. | 0.3 | C. | 0.8 | D. | 0.9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=12cm,BC=18cm,点P从点A出发以2cm/s的速度沿A→D→C运动,点P从点A出发1秒后,点Q从点C出发,并以1cm/s速度向点B运动,当点P到达点C时,点Q也停止运动.设点P的运动时间为t秒.
如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=12cm,BC=18cm,点P从点A出发以2cm/s的速度沿A→D→C运动,点P从点A出发1秒后,点Q从点C出发,并以1cm/s速度向点B运动,当点P到达点C时,点Q也停止运动.设点P的运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
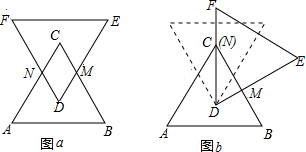
| A. | 2:1 | B. | 2:$\sqrt{3}$ | C. | 4:3 | D. | $\sqrt{3}$:$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
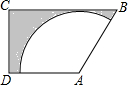 如图,梯形ABCD中,AD∥BC,∠C=90°,AB=AD=4,BC=6,以点A为圆心在梯形内画出一个最大的扇形,则阴影部分的面积为10$\sqrt{3}$-4π.
如图,梯形ABCD中,AD∥BC,∠C=90°,AB=AD=4,BC=6,以点A为圆心在梯形内画出一个最大的扇形,则阴影部分的面积为10$\sqrt{3}$-4π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
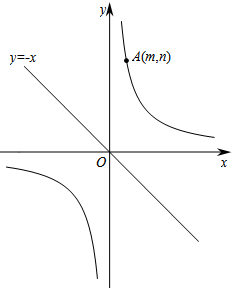 如图,已知直线y=-x和双曲线$y=\frac{k}{x}$(k>0),点A(m,n)(m>0)在双曲线$y=\frac{k}{x}$上.
如图,已知直线y=-x和双曲线$y=\frac{k}{x}$(k>0),点A(m,n)(m>0)在双曲线$y=\frac{k}{x}$上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
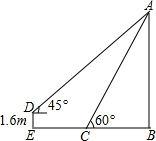 在升旗结束后,小明想利用所学数学知识测量学校旗杆高度,如图,旗杆的顶端垂下一绳子,将绳子拉直钉在地上,末端恰好至C处且与地面成60°角,小明从绳子末端C处拿起绳子放在头顶,后退至E点,此时绳子末端D与旗杆的顶端A成45°仰角,已知小明身高DE=1.6m,如图,求旗杆AB的高度和小明后退的距离.(单位:米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,结果保留一位小数)
在升旗结束后,小明想利用所学数学知识测量学校旗杆高度,如图,旗杆的顶端垂下一绳子,将绳子拉直钉在地上,末端恰好至C处且与地面成60°角,小明从绳子末端C处拿起绳子放在头顶,后退至E点,此时绳子末端D与旗杆的顶端A成45°仰角,已知小明身高DE=1.6m,如图,求旗杆AB的高度和小明后退的距离.(单位:米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,结果保留一位小数)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com