
 ,0),B为y轴上的一个动点,
,0),B为y轴上的一个动点, x+3上的一个动点,
x+3上的一个动点,

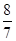 C(﹣
C(﹣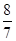 ,
, ) ②E(﹣
) ②E(﹣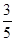 ,
, ),C(﹣
),C(﹣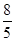 ,
, ),1
),1 ﹣0|=
﹣0|= ≠2,
≠2,

 x+3上的一个动点,点D的坐标是(0,1),
x+3上的一个动点,点D的坐标是(0,1), x0+3),
x0+3), x0+2,
x0+2,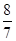 ,
,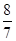 ,
,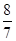 ,
, );
);
 x+3垂直的直线上时,点C与点E的“非常距离”最小,设E(x,y)(点E位于第二象限).则
x+3垂直的直线上时,点C与点E的“非常距离”最小,设E(x,y)(点E位于第二象限).则 ,
,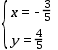 ,
,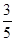 ,
, ).
).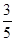 ﹣x0=
﹣x0= x0+3﹣
x0+3﹣ ,
,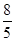 ,
,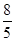 ,
, ),
), ﹣0|≥|0﹣y|,所以点A与点B的“非常距离”最小值为|﹣
﹣0|≥|0﹣y|,所以点A与点B的“非常距离”最小值为|﹣ ﹣0|=
﹣0|= ;
; x0+3),根据材料“若|x1﹣x2|≥|y1﹣y2|,则点P1与点P2的“非常距离”为|x1﹣x2|”可知,C、D两点的“非常距离”的最小值为﹣x0=
x0+3),根据材料“若|x1﹣x2|≥|y1﹣y2|,则点P1与点P2的“非常距离”为|x1﹣x2|”可知,C、D两点的“非常距离”的最小值为﹣x0= x0+2,据此可以求得点C的坐标;
x0+2,据此可以求得点C的坐标; x+3垂直的直线上时,点C与点E的“非常距离”最小,即E(﹣
x+3垂直的直线上时,点C与点E的“非常距离”最小,即E(﹣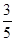 ,
, ).解答思路同上.
).解答思路同上.

 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源:不详 题型:解答题
 x+b,求n的值.
x+b,求n的值.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 与x轴、y轴分别交于点A、B,点C在线段AB上,且
与x轴、y轴分别交于点A、B,点C在线段AB上,且 .
. 上时,求该抛物线的表达式;
上时,求该抛物线的表达式;
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,CD=7.直线l经过A,D两点,且sin∠DAB=
,CD=7.直线l经过A,D两点,且sin∠DAB= .动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒5个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于AB,与折线A→D→C相交于点M,当P,Q两点中有一点到达终点时,另一点也随之停止运动.设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S.
.动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒5个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于AB,与折线A→D→C相交于点M,当P,Q两点中有一点到达终点时,另一点也随之停止运动.设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S.
 ?若存在,请求出t的值;若不存在,请说明理由;
?若存在,请求出t的值;若不存在,请说明理由;查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.x>-1 | B.x<-1 |
| C.x<-2 | D.无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com