
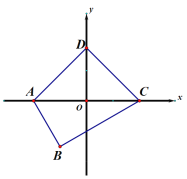
【题目】我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
(1)已知:如图,四边形ABCD是“等对角四边形”, ![]() ,则∠C= ;
,则∠C= ;
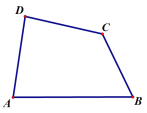
(2)已知:在“等对角四边形”ABCD中,∠DAB=60°,∠ABC=90°,AB=4 , AD=3.求对角线AC的长;
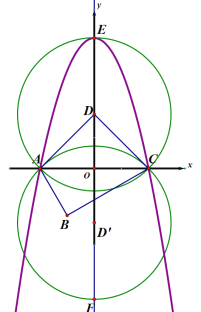
(3)已知:如图,在平面直角坐标系xoy中,四边形ABCD是“等对角四边形”,其中![]() ,点D在y轴上,抛物线
,点D在y轴上,抛物线![]() 过点A、C,点P在抛物线上,当满足
过点A、C,点P在抛物线上,当满足![]() 的P点至少有3个时,总有不等式
的P点至少有3个时,总有不等式![]() 成立,求n 的取值范围.
成立,求n 的取值范围.
【答案】(1)115°;(2)![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1)根据“等对角四边形”的概念即可求解;
(2)分两种情况:①当∠B=∠D=90°时延长AD,BC交于点E,先用含30°角的直角三角形的性质求出BE, DE,再用三角函数求出CE,即可得到BC,由勾股定理求出AC;②当∠A=∠C=60°时,过D分别作DE⊥AB于E,DF⊥BC于点F,先用含30°角的直角三角形的性质求出DE,CF,得到BC,由勾股定理求出AC;
(3)根据题意求出D(0,2),设抛物线解析式为![]() ,
,![]() ,以D(0,2)为圆心,AD长为半径作⊙D,以D’(0,-2)为圆心,AD长为半径作⊙D’,如图所示,⊙D交y轴正半轴于点E,⊙D’交y轴负半轴于点F.当点P在优弧AEC和优弧AFC上时
,以D(0,2)为圆心,AD长为半径作⊙D,以D’(0,-2)为圆心,AD长为半径作⊙D’,如图所示,⊙D交y轴正半轴于点E,⊙D’交y轴负半轴于点F.当点P在优弧AEC和优弧AFC上时![]() ,当抛物线过E点时满足题意的P点有3个,
,当抛物线过E点时满足题意的P点有3个,![]() ,当满足
,当满足![]() 的P点至少有3个时
的P点至少有3个时![]() ,依次求解即可.
,依次求解即可.
解:(1)由题意可得:∠B=∠D=85°,则∠C=360°-85°×2-75°=115°;
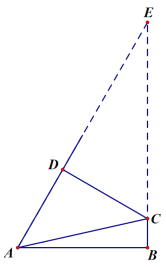
(2)①如图,∠B=∠D=90°时延长AD,BC交于点E
∵∠DAB=60°
∴∠E=30°
又 ∵AB=4,AD=3
∴![]()
∴![]()
∴![]()
∴![]()
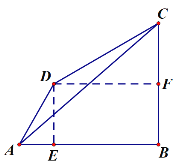
②如图,∠A=∠C=60°时,过D分别作DE⊥AB于E,DF⊥BC于点F
∵∠DAB=∠BCD=60°
又 ∵AB=4,AD=3
∴![]()
∴![]()
∴![]()
∴
综上,![]()
(3)∵![]()
∴![]()
∴![]()
∴∠ABC=90°
∵![]() ,
,
∴![]()
∵四边形ABCD是“等对角四边形”
∴![]()
∴D(0,2)
∵抛物线![]() 过点A、C,
过点A、C,
∴![]()
∴![]() ,
,![]()
以D(0,2)为圆心,AD长为半径作⊙D,以D’(0,-2)为圆心,AD长为半径作⊙D’,如图所示,⊙D交y轴正半轴于点E,⊙D’交y轴负半轴于点F.当点P在优弧AEC和优弧AFC上时![]() ,当抛物线过E点时满足题意的P点有3个,
,当抛物线过E点时满足题意的P点有3个,
此时,![]()
当满足![]() 的P点至少有3个时,
的P点至少有3个时,![]()
当![]() 时,
时,![]()
∵总有不等式![]() 成立
成立
∴![]()
∴![]()


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
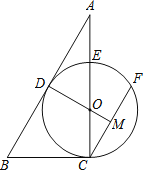
【题目】如图,在△ABC中,点O在边AC上,⊙O与△ABC的边BC,AB分别相切于C,D两点,与边AC交于E点,弦CF与AB平行,与DO的延长线交于M点.
(1)求证:点M是CF的中点;
(2)若E是![]() 的中点,BC=a,
的中点,BC=a,
①求![]() 的弧长;
的弧长;
②求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
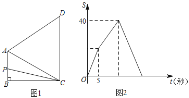
【题目】如图1,四边形ABCD中,AB∥CD,∠B=90°,AC=AD.动点P从点B出发沿折线B-A-D-C方向以1单位/秒的速度运动,在整个运动过程中,△BCP的面积S与运动时间t(秒)的函数图象如图2所示,则AD等于( )
A. 10B. ![]() C. 8D.
C. 8D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
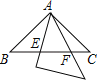
【题目】两个全等的等腰直角三角形,斜边长为2,按如图放置,其中一个三角形45°角的项点与另一个三角形的直角顶点A重合,若三角形ABC固定,当另一个三角形绕点A旋转时,它的角边和斜边所在的直线分别与边BC交于点E、F,设BF=![]() CE=
CE=![]() 则
则![]() 关于
关于![]() 的函数图象大致是( )
的函数图象大致是( )
A.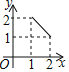 B.
B.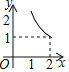 C.
C.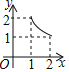 D.
D.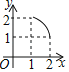
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx﹣2(a≠0)的图象的顶点在第三象限,且过点(1,0),设t=a﹣b﹣2,则t值的变化范围是( )
A. ﹣2<t<0 B. ﹣3<t<0 C. ﹣4<t<﹣2 D. ﹣4<t<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一空旷场地上设计一落地为矩形ABCD的小屋,AB+BC=10m,拴住小狗的10m长的绳子一端固定在B点处,小狗在不能进入小屋内的条件下活动,其可以活动的区域面积为S(m2).
(1)如图1,若BC=4m,则S=_____m2.
(2)如图2,现考虑在(1)中矩形ABCD小屋的右侧以CD为边拓展一正△CDE区域,使之变成落地为五边形ABCED的小屋,其他条件不变,则在BC的变化过程中,当S取得最小值时,边BC的长为____m.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学练习推铅球,铅球推出后在空中飞行的轨迹是一条抛物线,铅球在离地面1米高的A处推出,达到最高点B时的高度是2.6米,推出的水平距离是4米,铅球在地面上点C处着地
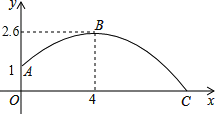
(1)根据如图所示的直角坐标系求抛物线的解析式;
(2)这个同学推出的铅球有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
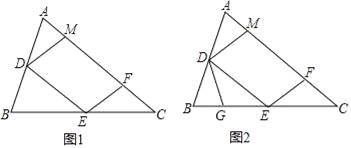
【题目】如图1,在锐角△ABC中,D、E分别是AB、BC的中点,点F在AC上,且满足∠AFE=∠A,DM∥EF交AC于点M.
(1)证明:DM=DA;
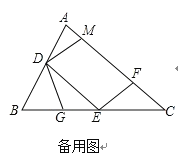
(2)如图2,点G在BE上,且∠BDG=∠C,求证:△DEG∽△ECF;
(3)在图2中,取CE上一点H,使得∠CFH=∠B,若BG=3,求EH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲车从A地到B地,乙车从B地到A地,乙车先出发先到达,甲乙两车之间的距离y(千米)与行驶的时间x(小时)的函数关系如图所示,则下列说法中不正确的是( )
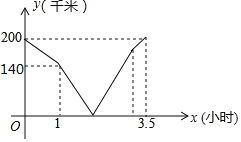
A.甲车的速度是80km/hB.乙车的速度是60km/h
C.甲车出发1h与乙车相遇D.乙车到达目的地时甲车离 B地10km
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com