
【题目】如图,将矩形ABCD沿MN折叠,使点B与点D重合. 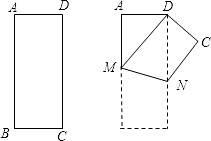
(1)求证:DM=DN;
(2)当AB和AD满足什么数量关系时,△DMN是等边三角形?并说明你的理由.
【答案】
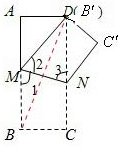
(1)证明:由题意知∠1=∠2,
又AB∥CD,得∠1=∠3,
则∠2=∠3.
故DM=DN
(2)解:当AB= ![]() AD时,△DMN是等边三角形.
AD时,△DMN是等边三角形.
证明:连接BD.
∵∠A=90°,AB= ![]() AD,
AD,
∴tan∠ABD= ![]() =
= ![]() ,
,
∴∠ABD=30°.
∵BM=MD,
∴∠ABD=∠MDB=30°,
∴∠BMD=120°.
∴∠1=∠2=60°.
又DM=DN,
∴△DMN是等边三角形.
【解析】(1)根据矩形对边平行得∠1=∠3,根据折叠的性质得∠1=∠2,所以∠2=∠3,得DM=DN;(2)假设△DMN是等边三角形,则∠ADM=30°.有MD=2AM,AD= ![]() AM,AB=3AM,得AB=
AM,AB=3AM,得AB= ![]() AD.
AD.
【考点精析】关于本题考查的等边三角形的判定和翻折变换(折叠问题),需要了解三个角都相等的三角形是等边三角形;有一个角等于60°的等腰三角形是等边三角形;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】某中学在安全工作月中,进行了“防自然灾害﹣地震知识知多少”专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,花粉等级后的数据整理如下表:
等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 |
频数 | 40 | 120 | n | 4 |
频率 | 0.2 | m | 0.18 | 0.02 |
(1)表中m的值为 , n的值为;
(2)根据表中的数据,请你计算“非常了解”的频率在如图中对应的扇形的圆心角的度数,并补全扇形统计图; 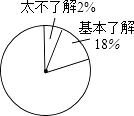
(3)若校一共有2400名学生,请根据调查结果估计全校学生中“比较了解”的人数为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察算式:1×3+1=4=22;2×4+1=9=32;3×5+1=16=42;4×6+1=25=52,…
(1)请根据你发现的规律填空:6×8+1=( )2;
(2)用含n的等式表示上面的规律: ;
(3)用找到的规律解决下面的问题:
计算:(1+![]() )(1+
)(1+![]() )(1+
)(1+![]() )(1+
)(1+![]() )…(1+
)…(1+![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温度的度量有两种基本单位:摄氏温度(℃),华氏温度(℉).在温度计上,摄氏温度x与华氏温度y有如下表所示的对应关系:
x/℃ | … | -10 | 0 | 10 | 20 | … |
y/℉ | … | 14 | 32 | 50 | 68 | … |
按下列步骤确定y与x之间的函数关系式.
(1)在平面直角坐标系中描点、连线,画出图象;
(2)猜想能表示y与x之间关系的函数类型;
(3)确定y与x之间的函数关系式,并验证你的想法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2﹣ ![]() x﹣2(a≠)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
x﹣2(a≠)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).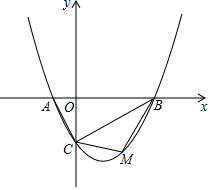
(1)求抛物线的解析式;
(2)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标;
(3)试探究:△ABC的外接圆的圆心位置,并求出圆心坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点M为直线AB上一动点, ![]() 都是等边三角形,连接BN
都是等边三角形,连接BN
![]() 求证:
求证: ![]() ;
;
![]() 分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系
分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系![]() 不需证明
不需证明![]() ;
;
![]() 如图4,当
如图4,当![]() 时,证明:
时,证明: ![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将背面相同,正面分别标有数字1,2,3,4的四张卡片洗匀后,背面朝上放在桌面上.
(1)从中随机抽取一张卡片,求该卡片正面上的数字是偶数的概率;
(2)先从中随机抽取一张卡片(不放回),将该卡片正面上的数字作为十位上的数字;再随机抽取一张,将该卡片正面上的数字作为个位上的数字,则组成的两位数恰好是4的倍数的概率是多少?请用树状图或列表法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在直角梯形ABCD中,AD∥BC,∠ADC=90°,BC= ![]() ,AD=
,AD= ![]() ,CD=12,过AB的中点E作AB的垂线交BC的延长线于F.
,CD=12,过AB的中点E作AB的垂线交BC的延长线于F. 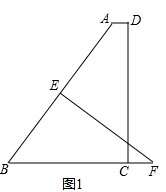
(1)求BF的长;
(2)如图2,以点C为原点,建立平面直角坐标系,请通过计算判断,过E点的反比例函数图象与直线AB是否还有另一个交点? 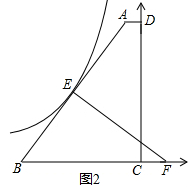
查看答案和解析>>
科目:初中数学 来源: 题型:
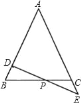
【题目】如图所示,在△ABC中,AB=AC,D为AB上一点,E为AC延长线上的一点,且CE=BD,连接DE交BC于点P.
(1)求证:PE=PD;
(2)若CE:AC=1:5,BC=10,求BP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com